Cước điện thoại \[y\] (nghìn đồng) là số tiền mà người sử dụng điện thoại cần trả hàng tháng, nó phục thuộc vào lượng thời gian gọi \[x\] (phút) của người đó trong tháng. Mỗi liên hệ giữa hai đại lượng này là một là số bậc nhất \[y = ax + b\]. Hãy tìm \[a,\,b\] biết rằng nhà bạn Nam trong tháng 5 đã gọi 100 phút với số tiền là 40 nghìn đồng và trong tháng 6 gọi 40 phút với số tiền là 28 nghìn đồng.
Cước điện thoại \[y\] (nghìn đồng) là số tiền mà người sử dụng điện thoại cần trả hàng tháng, nó phục thuộc vào lượng thời gian gọi \[x\] (phút) của người đó trong tháng. Mỗi liên hệ giữa hai đại lượng này là một là số bậc nhất \[y = ax + b\]. Hãy tìm \[a,\,b\] biết rằng nhà bạn Nam trong tháng 5 đã gọi 100 phút với số tiền là 40 nghìn đồng và trong tháng 6 gọi 40 phút với số tiền là 28 nghìn đồng.
Quảng cáo
Trả lời:
Theo đề ta có hệ phương trình \[\left\{ \begin{array}{l}100a + b = 40\\4a + b = 28\end{array} \right.\]
\[ \Leftrightarrow \left\{ \begin{array}{l}a = \frac{1}{5}\\b = 20\end{array} \right.\]
Vậy \[a = \frac{1}{5},\,b = 20\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải

a)
Ta có:\[JM = JE\] (tính chất hai tiếp tuyến cắt nhau) và \[OM = OE\] (bán kính).
\[ \Rightarrow OJ\] là đường trung trực của \[ME\].
Từ đó suy ra \[\Delta OMJ = \Delta OEJ\] (c – c – c).
\[ \Rightarrow \widehat {MOF} = \widehat {EOF}\]
Từ đó suy ra \[\Delta OMF = \Delta OEF\] (c – g – c).
\[ \Rightarrow \widehat {OMF} = \widehat {OEF}\].
b)
Ta có \[\widehat {OMI} = \widehat {ODI} = 90^\circ \] (định nghĩa tiếp tuyến tại điểm).
Suy ra tứ giác \[ODIM\] nội tiếp (1).
Xét tam giác \[\Delta OED\] có \[\widehat {OED} = \widehat {ODE}\] (do \[OD = OE = R\])
Theo ý a) ta có \[\widehat {OMF} = \widehat {OEF}\] nên ta có \[\widehat {ODE} = \widehat {ODF} = \widehat {OMF}\]
Suy ra tứ giác \[ODMF\] nội tiếp (do cùng chắn cung \[OF\]) (2).
Từ (1) và (2) suy ra 5 điểm \[I;\,D;\,O;\,F;\,M\]cùng nằm trên một đường tròn.
c)
+) Ta có tứ giác\[IDOF\]nội tiếp (do 5 điểm \[I;\,D;\,O;\,F;\,M\]cùng nằm trên một đường tròn).
\[ \Rightarrow \widehat {DIO} = \widehat {DFO}\] (cùng chắn cung DO )
\[ \Rightarrow \widehat {AIO} = \widehat {EFO}\] (2 góc kề bù tương ứng) (3)
Ta lại có tứ giác \[ADOE\] nội tiếp (do \[\widehat {ADO} = \widehat {AEO} = 90^\circ \])
\[ \Rightarrow \widehat {DAO} = \widehat {DEO}\] (4)
Từ (3) và (4) suy ra (g – g).
\[ \Rightarrow \widehat {IOA} = \widehat {EOF}\]
Mà \[\widehat {EOF} = \widehat {JOM}\]
Nên \[\widehat {IOA} = \widehat {JOM}\].
+) Ta có \[\sin \widehat {IOA} = \sin \widehat {JOM} = \frac{{MJ}}{{OJ}}\] (5).
Mặt khác \[JMFO\] nội tiếp (do ý b) nên ta có \[\widehat {JMF} = \widehat {JOI}\].
Suy ra (g – g) \[ \Rightarrow \frac{{MJ}}{{JO}} = \frac{{MF}}{{OI}}\](6)
Từ (5) và (6) suy ra \[\sin \widehat {IOA} = \frac{{MF}}{{IO}}\].
Lời giải
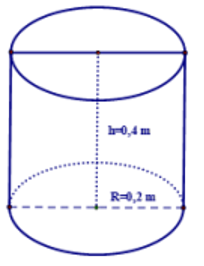
a) Thể tích 1 cái thùng hình trụ là
\[{V_{tru}} = \pi {R^2}h = \pi {.0,2^2}.0,4 \approx 0,05\,\,\left( {{{\rm{m}}^{\rm{3}}}} \right)\]
Lượng nước anh Minh đổ vào hồ trong mỗi lần gánh là
\[{V_g} = 2{V_{tru}}.90\% \approx 0,09\,\,\left( {{{\rm{m}}^{\rm{3}}}} \right)\].
b) Thể tích cái hồ là: \[V = 2.2.1 = 4\,\,\left( {{{\rm{m}}^{\rm{3}}}} \right)\]
Ta có: \[4:0,09 \approx 44,44\]
Vậy anh Minh cần gánh ít nhất 45 lần để đầy hồ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.