Cho hình phẳng có số liệu như hình vẽ. Tính độ dài đoạn thẳng $AE$.

$Cho hình phẳng có số liệu như hình vẽ. Tính độ dài đoạn thẳng $AE$. (ảnh 1)$

Xem lời giải

Câu hỏi trong đề: Đề thi tuyển sinh vào lớp 10 môn Toán năm 2023-2024 Chuyên Tây Ninh có đáp án !!

Quảng cáo

Trả lời:

Giải bởi Vietjack

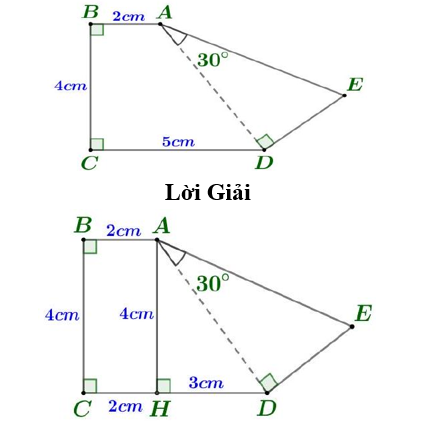
Kẻ $AH \bot CD$.

Suy ra: $ABCH$ là hình chữ nhật$ \Rightarrow AH = 4{\rm{\;}}cm;HD = CD - CH = 3{\rm{\;}}cm$.

Xét ${\rm{\Delta }}AHD\left( {\hat H = {{90}^ \circ }} \right)$ có: $A{D^2} = A{H^2} + H{D^2} = {4^2} + {3^2} = 25 \Rightarrow AD = 5{\rm{\;}}cm$.

Xét ${\rm{\Delta }}ADE\left( {\widehat {ADE} = {{90}^ \circ }} \right)$ có: $cos{30^ \circ } = \frac{{AD}}{{AE}} \Rightarrow AE = \frac{{AD}}{{cos{{30}^ \circ }}} = \frac{{10}}{{\sqrt 3 }} = \frac{{10\sqrt 3 }}{3}$.

Vậy $AE = \frac{{10\sqrt 3 }}{3}$

Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho $a,b,c$ là ba số thực khác 0 thỏa mãn $\frac{{2a}}{b} = \frac{{3b}}{c} = \frac{c}{{6a}}$. Tính giá trị của biểụ thức $P = \frac{{4ac - cb}}{{bc + 2ab}}$

Xem đáp án

Lời giải

Đặt: $\frac{{2a}}{b} = \frac{{3b}}{c} = \frac{c}{{6a}} = t \Rightarrow \left\{ {\begin{array}{*{20}{l}}{2a = bt}\\{b = \frac{c}{3}t = 2a{t^2} \Leftrightarrow 2a = 2a{t^3} \Leftrightarrow t = 1.}\\{c = 6at}\end{array}} \right.$

Suy ra: $\left\{ {\begin{array}{*{20}{l}}{b = 2a}\\{c = 6a}\end{array}} \right.$.

$P = \frac{{4ac - cb}}{{bc + 2ab}} = \frac{{4a.6a - 6a.2a}}{{2a.6a + 2a.2a}} = \frac{{12}}{{16}} = \frac{3}{4}$

Câu 2

Cho $a,b,c$ là các số thực dương thỏa mãn $a + b + c \ge 6$. Tìm giá trị nhỏ nhất của biểu thức $M = \frac{1}{6}\left( {19a + 22b + 25c} \right) + 2\left( {\frac{5}{a} + \frac{6}{b} + \frac{7}{c}} \right)$.

Xem đáp án

Lời giải

Ta có: $a + b + c \ge 6$.

$M = \frac{1}{6}\left( {19a + 22b + 25c} \right) + 2\left( {\frac{5}{a} + \frac{6}{b} + \frac{7}{c}} \right) = \left( {\frac{{19}}{6}a + \frac{{10}}{a}} \right) + \left( {\frac{{22}}{6}b + \frac{{12}}{b}} \right) + \left( {\frac{{25}}{6}c + \frac{{14}}{c}} \right)$

Xét $k,m,n > 0:ka + \frac{{10}}{a} \ge 2\sqrt {10k} ;mb + \frac{{12}}{b} \ge 2\sqrt {12m} ;nc + \frac{{14}}{c} \ge 2\sqrt {14n} $

$a = 2 \Rightarrow 2k + 5 \ge 2\sqrt {10k} $

Dấu bằng xảy ra $ \Leftrightarrow ka = \frac{{10}}{a} \Rightarrow 2k = 5 \Leftrightarrow k = \frac{5}{2}$.

Tương tự ta tìm được: $m = 3,n = \frac{7}{2}$.

Do đó: $M = \left( {\frac{5}{2}a + \frac{{10}}{a}} \right) + \left( {3b + \frac{{12}}{b}} \right) + \left( {\frac{7}{2}c + \frac{{14}}{c}} \right) + \frac{2}{3}a + \frac{2}{3}b + \frac{2}{3}c$

$ \Rightarrow M \ge 2\sqrt {25} + 2\sqrt {36} + 2\sqrt {49} + \frac{2}{3} \cdot 6 = 40$.

Dấu bằng xảy ra khi $a = b = c = 2$.

Vậy ${M_{Min}} = 40$ khi $a = b = c = 2$.

Câu 3