Cho đường tròn \(\left( O \right)\) và điểm \(M\) nằm ngoài \(\left( O \right)\), vẽ tiếp tuyến \(MA\) và cát tuyến \(MBC\) không đi qua \(O\left( {MB < MC} \right)\). Gọi \(H\) là hình chiếu vuông góc của \(A\) trên \(MO\).
a) (1,0 điểm) Chứng minh: Tứ giác \(BHOC\) nội tiếp.
b) (1,0 điểm) Vẽ đường thẳng qua \(B\) song song với \(AC\) cắt các đường thẳng \(MA,AH\) lần lượt tại \(K,I\). Chứng minh \(KB = BI\).
Cho đường tròn \(\left( O \right)\) và điểm \(M\) nằm ngoài \(\left( O \right)\), vẽ tiếp tuyến \(MA\) và cát tuyến \(MBC\) không đi qua \(O\left( {MB < MC} \right)\). Gọi \(H\) là hình chiếu vuông góc của \(A\) trên \(MO\).
a) (1,0 điểm) Chứng minh: Tứ giác \(BHOC\) nội tiếp.
b) (1,0 điểm) Vẽ đường thẳng qua \(B\) song song với \(AC\) cắt các đường thẳng \(MA,AH\) lần lượt tại \(K,I\). Chứng minh \(KB = BI\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
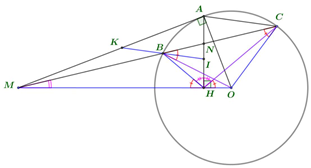
Ta có: \(\Delta MBA \sim \Delta MAC\) (g-g) \(\frac{{MA}}{{MC}} = \frac{{MB}}{{MA}} \Rightarrow M{A^2} = MB.MC\).
\(\Delta MAO\left( {\hat A = {{90}^ \circ }} \right),AH \bot MO \Rightarrow M{A^2} = MH.MO\)
Suy ra: \(MB \cdot MC = MH \cdot MO \Rightarrow \frac{{MB}}{{MO}} = \frac{{MH}}{{MC}}\).
Xét \(\Delta BMH\) và \(\Delta OMC\) có \(\hat M\) chung và \(\frac{{MB}}{{MO}} = \frac{{MH}}{{MC}} \Rightarrow {\rm{\Delta }}BMH \sim {\rm{\Delta }}OMC\) (c-g-c).
Suy ra: \(\widehat {BHM} = \widehat {BCO}\) mà \(\widehat {BHM} + \widehat {BHO} = {180^ \circ } \Rightarrow \widehat {BCO} + \widehat {BHO} = {180^ \circ }\).
Vậy tứ giác \(BHOC\) nội tiếp.
b)
\(BK\parallel AC \Rightarrow \frac{{BK}}{{AC}} = \frac{{MB}}{{MC}}\)
\(BI\parallel AC \Rightarrow \frac{{BI}}{{AC}} = \frac{{BN}}{{NC}}\)
Do \(OHBC\) nội tiếp đường tròn nên: \(\widehat {OHC} = \widehat {OBC} = \widehat {OCB} = \widehat {BHM}\).
Khi đó: \(\left. {\begin{array}{*{20}{c}}{\widehat {AHC} + \widehat {OHC} = {{90}^0}}\\{\;\widehat {AHB} + \widehat {BHM} = {{90}^0}}\end{array}} \right\} \Rightarrow \widehat {AHC} = \widehat {AHB} \Rightarrow AH\) là phân giác trong của \(\widehat {BHC}\)
\( \Rightarrow \frac{{HB}}{{HC}} = \frac{{BN}}{{NC}}\)
Mà \(HM \bot AH \Rightarrow HM\) là phân giác ngoài của \(\widehat {BHC} \Rightarrow \frac{{HB}}{{HC}} = \frac{{MB}}{{MC}}\left( {{\rm{**}}} \right)\).
Từ \(\left( 1 \right),\left( 2 \right),\left( {\rm{*}} \right),\left( {{\rm{**}}} \right) \Rightarrow \frac{{BK}}{{AC}} = \frac{{BI}}{{AC}} \Rightarrow BK = BI\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đặt: \(\frac{{2a}}{b} = \frac{{3b}}{c} = \frac{c}{{6a}} = t \Rightarrow \left\{ {\begin{array}{*{20}{l}}{2a = bt}\\{b = \frac{c}{3}t = 2a{t^2} \Leftrightarrow 2a = 2a{t^3} \Leftrightarrow t = 1.}\\{c = 6at}\end{array}} \right.\)
Suy ra: \(\left\{ {\begin{array}{*{20}{l}}{b = 2a}\\{c = 6a}\end{array}} \right.\).
\(P = \frac{{4ac - cb}}{{bc + 2ab}} = \frac{{4a.6a - 6a.2a}}{{2a.6a + 2a.2a}} = \frac{{12}}{{16}} = \frac{3}{4}\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Ta có: \(a + b + c \ge 6\).
\(M = \frac{1}{6}\left( {19a + 22b + 25c} \right) + 2\left( {\frac{5}{a} + \frac{6}{b} + \frac{7}{c}} \right) = \left( {\frac{{19}}{6}a + \frac{{10}}{a}} \right) + \left( {\frac{{22}}{6}b + \frac{{12}}{b}} \right) + \left( {\frac{{25}}{6}c + \frac{{14}}{c}} \right)\)
Xét \(k,m,n > 0:ka + \frac{{10}}{a} \ge 2\sqrt {10k} ;mb + \frac{{12}}{b} \ge 2\sqrt {12m} ;nc + \frac{{14}}{c} \ge 2\sqrt {14n} \)
\(a = 2 \Rightarrow 2k + 5 \ge 2\sqrt {10k} \)
Dấu bằng xảy ra \( \Leftrightarrow ka = \frac{{10}}{a} \Rightarrow 2k = 5 \Leftrightarrow k = \frac{5}{2}\).
Tương tự ta tìm được: \(m = 3,n = \frac{7}{2}\).
Do đó: \(M = \left( {\frac{5}{2}a + \frac{{10}}{a}} \right) + \left( {3b + \frac{{12}}{b}} \right) + \left( {\frac{7}{2}c + \frac{{14}}{c}} \right) + \frac{2}{3}a + \frac{2}{3}b + \frac{2}{3}c\)
\( \Rightarrow M \ge 2\sqrt {25} + 2\sqrt {36} + 2\sqrt {49} + \frac{2}{3} \cdot 6 = 40\).
Dấu bằng xảy ra khi \(a = b = c = 2\).
Vậy \({M_{Min}} = 40\) khi \(a = b = c = 2\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập