Một khối sắt hình cầu được làm bằng sắt nguyên chất, đặc ruột có giá trị diện tích mặt cầu (tính bằng m2) gấp 3 lần giá trị thể tích của khối cầu đó (tính bằng m3). Hỏi khối cầu sắt đó nặng bao nhiêu kilogram? (Biết rằng khối lượng riêng của sắt là \(7800\;{\rm{kg}}/{{\rm{m}}^3}\) và lấy \(\pi = 3,14).\)
Một khối sắt hình cầu được làm bằng sắt nguyên chất, đặc ruột có giá trị diện tích mặt cầu (tính bằng m2) gấp 3 lần giá trị thể tích của khối cầu đó (tính bằng m3). Hỏi khối cầu sắt đó nặng bao nhiêu kilogram? (Biết rằng khối lượng riêng của sắt là \(7800\;{\rm{kg}}/{{\rm{m}}^3}\) và lấy \(\pi = 3,14).\)
Câu hỏi trong đề: Đề thi minh họa Toán vào 10 năm học 2025 - 2026 Thái Bình !!
Quảng cáo
Trả lời:
Gọi bán kính của khối cầu là \(r{\rm{\;(m)}},\,\,r > 0.\)
Khi đó:
⦁ Diện tích mặt cầu của khối cầu là: \[S = 4\pi {r^2}{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
⦁ Thể tích của khối cầu là: \(V = \frac{4}{3}\pi {r^3}{\rm{\;(}}{{\rm{m}}^3}{\rm{)}}{\rm{.}}\)
Vì giá trị diện tích mặt cầu (tính bằng m2) gấp 3 lần giá trị thể tích của khối cầu đó (tính bằng m3) nên ta có:
\(4\pi {r^2} = 3 \cdot \frac{4}{3}\pi {r^3},\) suy ra \(r = 1{\rm{\;(m)}}{\rm{.}}\)
Do đó thể tích của khối cầu là \(V = \frac{4}{3} \cdot 3,14 \cdot {1^3} = \frac{{314}}{{75}}{\rm{\;(}}{{\rm{m}}^3}{\rm{)}}{\rm{.}}\)
Vậy khối lượng của khối cầu sắt là: \(m = \frac{{314}}{{75}} \cdot 7\,\,800 = 32\,\,656\,\,({\rm{kg}}).\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Xét parabol \(y = m{x^2}\,\,\left( {m < 0} \right)\) trong mặt phẳng tọa đô \[Oxy\] như hình vẽ.
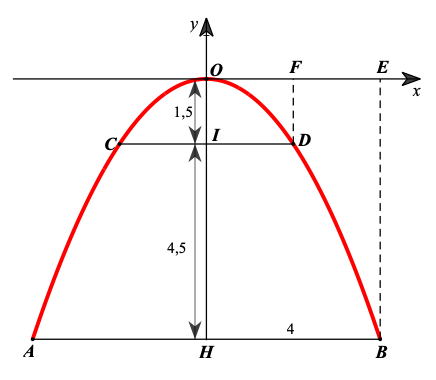
Vì Parabol nhận \[Oy\]làm trục đối xứng nên \(HB = 4\;{\rm{m}}\) hay \(OE = 4\;{\rm{m}}\)
Độ cao của cổng là 6 m nên \(OH = 6\;{\rm{m}}\) suy ra \(B\left( {4;\,\, - 6} \right)\)
Vì \(B\) thuộc parabol nên ta có \( - 6 = m \cdot {4^2}\) hay \(m = \frac{{ - 3}}{8}.\) Suy ra \(y = \frac{{ - 3}}{8}{x^2}.\)
Thanh sắt đặt nằm ngang ở độ cao \(4,5\;\;{\rm{m}}\) so với mặt đất nên ta có \(IH = 4,5\;{\rm{m}}\) suy ra \(OI = OH - IH = 6 - 4,5 = 1,5{\rm{\;(m)}}{\rm{.}}\)
Đặt \[OF = x\,\,({\rm{m}});\,\,\,x > 0.\]
Ta có \(D\left( {x; - 1,5} \right)\) thuộc parabol nên \( - 1,5 = \frac{{ - 3}}{8}{x^2}.\) Suy ra \(x = 2.\)
Hay \[ID = 2\;{\rm{m}}{\rm{.}}\] Suy ra \(CD = 4\;{\rm{m}}{\rm{.}}\)
Vậy độ dài của thanh sắt là 4 m.
Lời giải
Gọi giá niêm yết của đôi giày và chiếc vợt lần lượt là \(x,\,\,y\) triệu đồng \[\left( {x,\,\,y > 0} \right).\]
Vì tổng số tiền theo giá niêm yết của hai mặt hàng là 2,4 triệu đồng nên ta có phương trình: \(x + y = 2,4.\)
Giá 1 đôi giày thể thao sau giảm giá là: \(x - 10\% x = 90\% x = 0,9x\) (triệu đồng).
Giá 1 chiếc vợt sau giảm giá là: \(y - 15\% y = 85\% y = 0,85y\) (triệu đồng).
Vì anh Khánh trả cho cửa hàng 3,2 triệu đồng khi mua 1 đôi giày thể thao và 2 chiếc vợt theo chương trình khuyến mại nên ta có phương trình: \(0,9x + 2 \cdot 0,85y = 3,2.\)
Ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{x + y = 2,4}\\{0,9x + 2 \cdot 0,85y = 3,2}\end{array}} \right..\)
Giải hệ phương trình trên, ta được: \(\left\{ {\begin{array}{*{20}{l}}{x = 1,1}\\{y = 1,3}\end{array}} \right.\). Các giá trị thoả mãn điều kiện.
Vậy giá niêm yết của đôi giày là 1,1 triệu đồng, của chiếc vợt là 1,3 triệu đồng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.