(4,0 điểm)

Một hình nón có độ dài đường sinh bằng 50 cm và bán kính đáy bằng 30cm. Tính thể tích của hình nón đó ( lấy \[\pi  \approx 3,14\]).

Vì \(CF \bot AB\) nên \(\widehat {CFB} = 90^\circ \) suy ra tam giác BFC vuông tại F

Vì \(BE \bot AC\) nên \(\widehat {BEC} = 90^\circ \) suy ra tam giác BEC vuông tại E

Gọi O’ là trung điểm đoạn \(BC.\)

Xét tam giác BEC vuông tại E, O’ là trung điểm đoạn \(BC.\) . Suy ra  (tính chất đường trung tuyến trong tam giác vuông.)       (1)

Xét tam giác BFC vuông tại F, O’ là trung điểm đoạn \(BC.\) . Suy ra  ( tính chất đường trung tuyến trong tam giác vuông.)       (2)

Từ (1) và (2) suy ra mà O là tâm đường tròn ngoại tiếp tứ giác \(BFEC\), suy ra \(O\) trùng O’

Suy ra \(O\)là trung điềm đoạn \(BC.\).

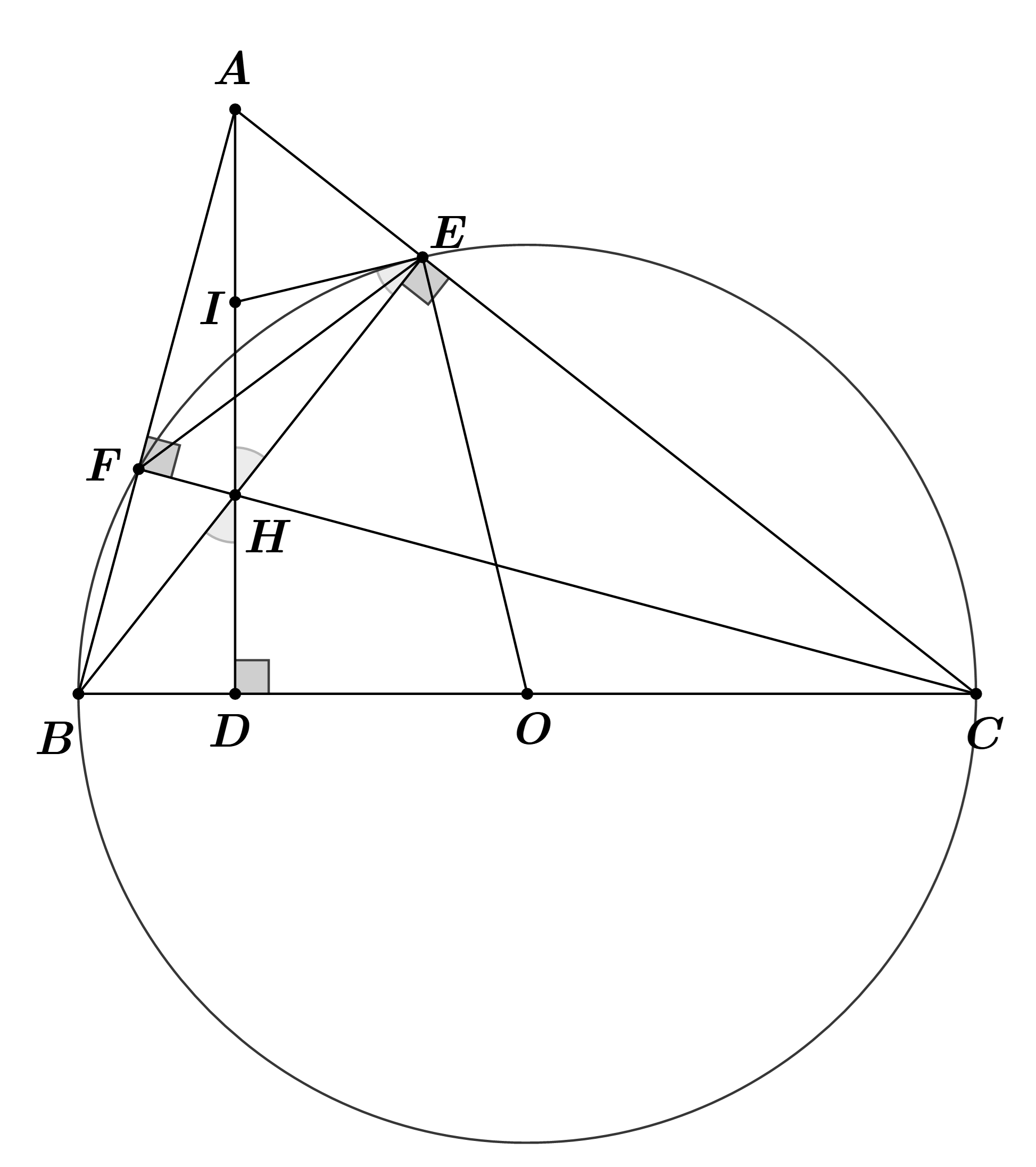
Xét \(\Delta AEH\) vuông tại \(H\), có \(EI\) là đường trung tuyến ứng với cạnh \(AH\) nên \(EI = \frac{1}{2}AH = IH\)

Suy ra: \(\Delta IEH\) cân tại \[I\] \( \Rightarrow \widehat {IEH} = \widehat {IHE}\)

Mà \(\widehat {IHE} = \widehat {BHD}\) (Hai góc đối đỉnh)

Suy ra: \(\widehat {IEH} = \widehat {BHD}\) (1)

Ta lại có: \(OB = OE = R\) \( \Rightarrow \Delta OEB\) cân tại \(O\)

\( \Rightarrow \widehat {OBE} = \widehat {OEB}\) (2)

Từ (1) và (2), ta có: \(\widehat {IEH} + \widehat {OEB} = \widehat {BHD} + \widehat {OBE}\)

Mặt khác: \(\widehat {BHD} + \widehat {OBE} = 90^\circ \) (vì \(\Delta BHD\) vuông tại \(D\))

Suy ra: \(\widehat {IEH} + \widehat {OEB} = \widehat {BHD} + \widehat {OBE} = 90^\circ \) hay \(\widehat {OEI} = 90^\circ \)

\( \Rightarrow OE \bot EI\)và \(E \in (O)\)Do đó: \(IE\) là tiếp tuyến của đường tròn \((O)\).

c) Vẽ \(CI\) cắt đường tròn \((O)\) tại \(M\,(M\) khác \(C\) ), \(EF\) cắt \(AD\) tại \(K\). Chứng minh ba điểm \(B,K,M\) thẳng hàng.

Ta có: góc BMC là góc nội tiếp chắn nửa đường tròn nên góc BMC = 90 độ

\( \Rightarrow BM \bot IC\)

Xét \(\Delta IEK\) và \(\Delta IDE\) có:

\(\widehat {EIK}\) là góc chung

\(\widehat {IDE} = \widehat {IEK}\,( = \widehat {ECF})\)

Do đó: (g.g)

\( \Rightarrow \frac{{IE}}{{ID}} = \frac{{IK}}{{IE}} \Rightarrow ID.IK = I{E^2}\)

Mặt khác: \(IM.IC = I{E^2}\) (Bạn đọc tự chứng minh)

\( \Rightarrow ID.IK = IM.IC\)

\( \Rightarrow \frac{{IM}}{{ID}} = \frac{{IK}}{{IC}}\)

Xét tam giác IMK và tam giác IDC có:

Góc MIK là góc chung

\(\frac{{IM}}{{ID}} = \frac{{IK}}{{IC}}\)

\( \Rightarrow \widehat {KMI} = \widehat {CDI} = 90^\circ \)

\( \Rightarrow KM \bot IC\)

\(\left. \begin{array}{l}BM \bot IC\\KM \bot IC\end{array} \right\} \Rightarrow B,M,K\) thẳng hàng