(4,0 điểm)
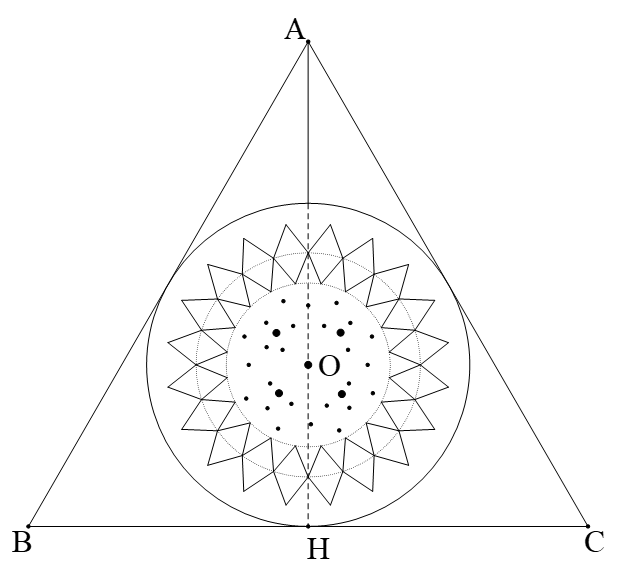
(1,0 điểm) Đài phun nước ở Công viên Hồ Khánh Hội, TP HCM códạng đường tròn (gọi là đường tròn tâm \[O\]) và được thiết kếtheo hình dáng những cánh hoa đan xen nhau, bên dưới là hệthống phun nước với nhiều độ cao khác nhau kết hợp với hệthống chiếu sáng và âm nhạc cùng các mảng cây xanh tạokhông gian đô thị vui tươi, sinh động.
Một học sinh vẽ tam giác đều \[ABC\] ngoại tiếp đường tròn\[\left( O \right)\]và tính được diện tích tam giác đều là \[1\,200\]m2. Bạn hãy tính bán kính và chu vi của đường tròn \[\left( O \right)\] (Kết quả làm tròn một chữ số thập phân và p = 3,14).
(4,0 điểm)
(1,0 điểm) Đài phun nước ở Công viên Hồ Khánh Hội, TP HCM códạng đường tròn (gọi là đường tròn tâm \[O\]) và được thiết kếtheo hình dáng những cánh hoa đan xen nhau, bên dưới là hệthống phun nước với nhiều độ cao khác nhau kết hợp với hệthống chiếu sáng và âm nhạc cùng các mảng cây xanh tạokhông gian đô thị vui tươi, sinh động.
Một học sinh vẽ tam giác đều \[ABC\] ngoại tiếp đường tròn\[\left( O \right)\]và tính được diện tích tam giác đều là \[1\,200\]m2. Bạn hãy tính bán kính và chu vi của đường tròn \[\left( O \right)\] (Kết quả làm tròn một chữ số thập phân và p = 3,14).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi \[O\] là tâm đường tròn nội tiếp \[\Delta ABC\].
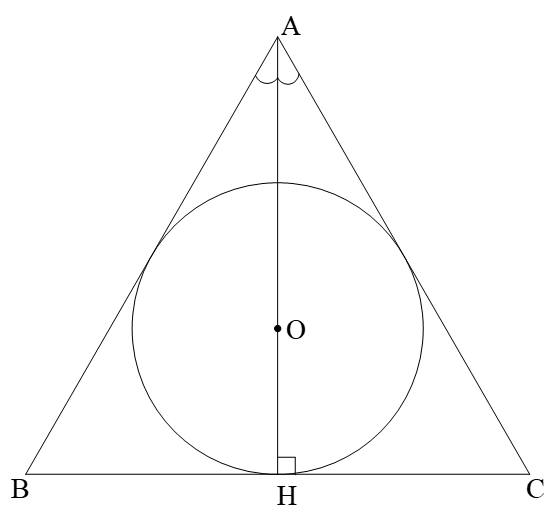
Khi đó \[O\] là giao điểm 3 đường phân giác.
Mà \[\Delta ABC\] đều nên \[AH\]là đường phân giác cũng là đường cao, đường trung tuyến.
Do đó \[O\] là trọng tâm \[\Delta ABC\] và \[AH = 3.OH = 3.R\].
và \[\widehat {HAC} = \frac{{\widehat {BAC}}}{2} = {30^0};\,\,BC = 2.HC\]
Xét \[\Delta HAC\]vuông tại \[H\]ta có
\[HC = AH.\tan 30^\circ = 3R.\frac{{\sqrt 3 }}{3} = R.\sqrt 3 \]
\[{S_{ABC}} = \frac{1}{2}AH.BC = AH.HC = 3R.R\sqrt 3 {\rm{ = 3}}\sqrt 3 {R^2}\]
\[1\,200\,\, = \,\,3\sqrt 3 .{R^2}\,\]
\[R{\rm{ = }}\sqrt {\frac{{1200}}{{3\sqrt 3 }}} \,\, \approx 15,2\,\,\,\,\,\left( {\rm{m}} \right)\]
Chu vi đường tròn (O) là \[2.3,14.15,2 \approx 95,5\](m)
Vậy bán kính \[\left( O \right)\]là \[15,2\]m; chu vi là \[95,5\]m.
Câu hỏi cùng đoạn
Câu 2:
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O. Các đường cao AD, BE, CF của tam giác ABC cắt nhau tại H.
a) Chứng minh bốn điểm A, B, D, E cùng thuộc một đường tròn.
b) Chứng minh \[DB.DC = DH.DA\].
c) Đường thẳng AO cắt đường tròn tâm O tại điểm K khác điểm A. Gọi I là giao điểm của hai đường thẳng HK và BC. Chứng minh I là trung điểm của đoạn thẳng BC.
d) Tính \[\frac{{AH}}{{AD}} + \frac{{BH}}{{BE}} + \frac{{CH}}{{CF}}\].
Giải bởi Vietjack
(0,75 điểm)
Ta có:\[\widehat {ADB} = {90^0}\] ( vì \[AD \bot BC\]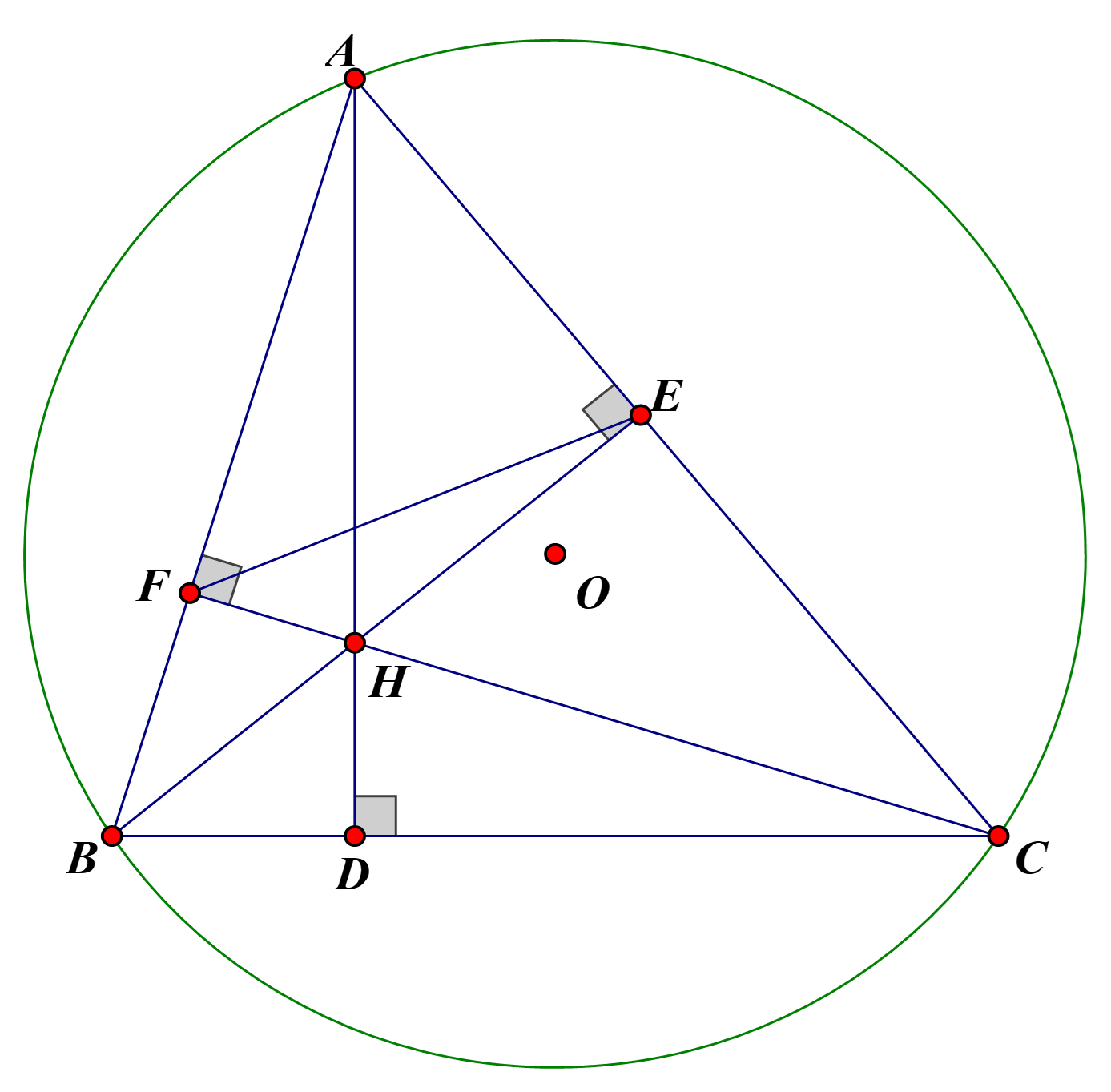 
\[\widehat {AEB} = {90^0}\] (vì \[BE \bot AC\])
Xét tứ giác ABDF có \[\widehat {ADB} = \widehat {AEB} = {90^0}\]
mà D và F là 2 đỉnh kề nhau cùng cạnh AB
dưới 1 góc vuông
Nên 4 điểm A, B, D, E cùng thuộc một đường tròn.
b) (0,75 điểm) Xét đường tròn ngoại tiếp tứ giác ABDF có
\[\widehat {EBD}\]là góc nội tiếp chắn cung DE
\[\widehat {EAD}\]là góc nội tiếp chắn cung DE
Nên \[\widehat {EBD} = \widehat {EAD}\](Hệ quả góc nội tiếp) hay \[\widehat {HBD} = \widehat {CAD}\]
Xét ΔBHD và ΔACD có\[\widehat {HDB} = \widehat {CDA} = {90^0}\]
\[\widehat {HBD} = \widehat {CAD}\] (cmt)
Do đó \[\Delta BHD\] đồng dạng với\[\Delta ACD\] (g-g)
Suy ra \[\frac{{DB}}{{AD}} = \frac{{DH}}{{DC}}\] => DB.DC = DH.DA
c) (0,75 điểm) Chứng minh I là trung điểm của đoạn thẳng BC.
(0,75 điểm) Chứng minh I là trung điểm của đoạn thẳng BC.
Xét đường tròn (O) có:
\(\widehat {ABK} = {90^0}\) (góc nội tiếp chắn nửa đường tròn), do đó
\(KB \bot AB\).
Mặt khác:\(CH \bot AB\) (giả thiết)
Suy ra:\(KB\)//\(CH\) (quan hệ vuông góc song song) (1)
Xét đường tròn (O) có:\(\widehat {ACK} = {90^0}\) (góc nội tiếp chắn
nửa đường tròn), do đó \(KC \bot AC\).
Mặt khác:\(BH \bot AC\) (giả thiết)
Suy ra: \(KC\)//\(BH\) (quan hệ vuông góc song song) (2)
Từ (1) và (2) suy ra tứ giác BHCK là hình bình hành
(dấu hiệu nhận biết), suy ra hai đường chéo BC và HK
cắt nhau tại trung điểm mỗi đường (tính chất).
Mà I là giao điểm của BC và HK nên I là trung điểm
của BC.
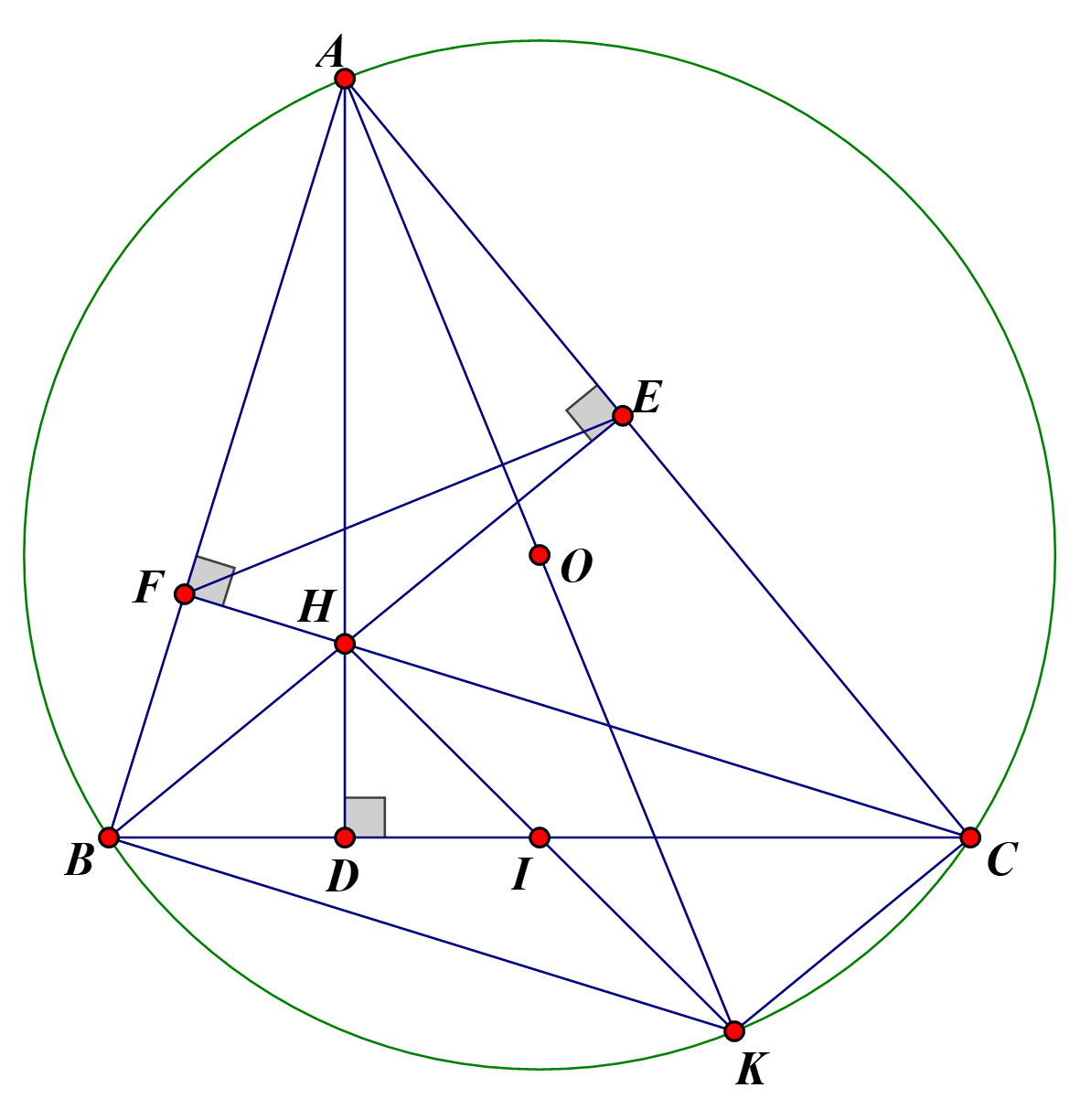
d) (0,75 điểm) Tính \[\frac{{AH}}{{AD}} + \frac{{BH}}{{BE}} + \frac{{CH}}{{CF}}\].
Đặt \(P = \frac{{AH}}{{AD}} + \frac{{BH}}{{BE}} + \frac{{CH}}{{CF}}\)
Khi đó
\(\begin{array}{l}P = \frac{{AD - HD}}{{AD}} + \frac{{BE - HE}}{{BE}} + \frac{{CF - HF}}{{CF}}\\P = 1 - \frac{{HD}}{{AD}} + 1 - \frac{{HE}}{{BE}} + 1 - \frac{{HF}}{{CF}}\\P = 3 - \left( {\frac{{HD}}{{AD}} + \frac{{HE}}{{BE}} + \frac{{HF}}{{CF}}} \right)\end{array}\)
Ta có: \(\frac{{HD}}{{AD}} = \frac{{\frac{1}{2}HD \cdot BC}}{{\frac{1}{2}AD \cdot BC}} = \frac{{{S_{\Delta ABC}}}}{{{S_{\Delta ABC}}}}\)
Chứng minh tương tự ta có:
\(\frac{{HE}}{{BE}} = \frac{{{S_{\Delta HAC{\rm{ }}}}}}{{{S_{\Delta ABC}}}};\,\,\,\,\frac{{HF}}{{CF}} = \frac{{{S_{\Delta HAB}}}}{{{S_{\Delta ABC}}}}\) \(\frac{{HD}}{{AD}} + \frac{{HE}}{{BE}} + \frac{{HF}}{{CF}} = \frac{{{S_{\Delta HBC}}}}{{{S_{\Delta ABC}}}} + \frac{{{S_{\Delta HAC}}}}{{{S_{ABC}}}} + \frac{{{S_{\Delta HAB}}}}{{{S_{AABC}}}} = \frac{{{S_{\Delta HBC}} + {S_{\Delta HAC}} + {S_{\Delta HAB}}}}{{{S_{ABC}}}} = \frac{{{S_{ABC}}}}{{{S_{\Delta BC}}}} = 1\)
Vậy \(P = \frac{{AH}}{{AD}} + \frac{{BH}}{{BE}} + \frac{{CH}}{{CF}} = 3 - 1 = 2\)
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
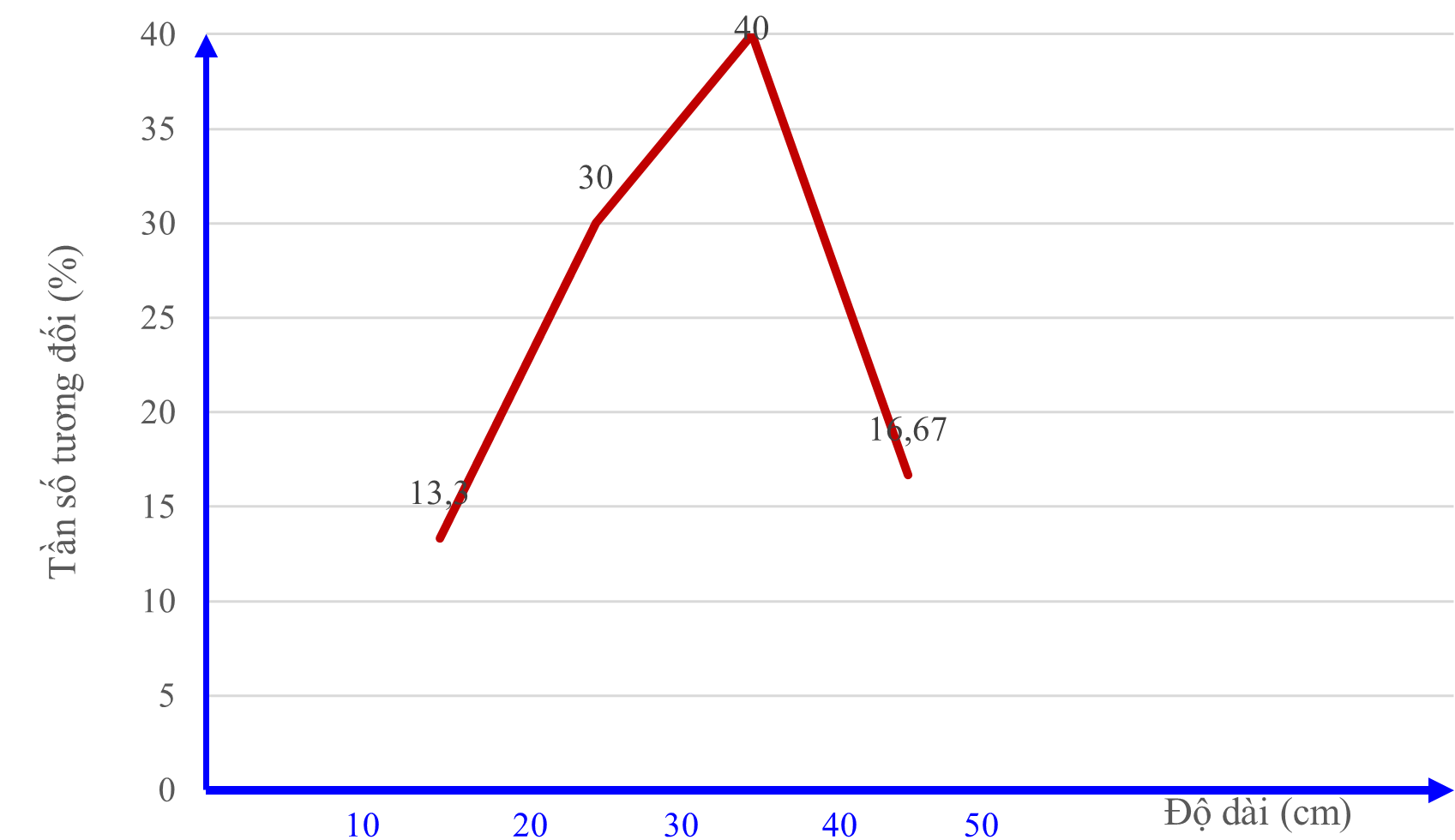
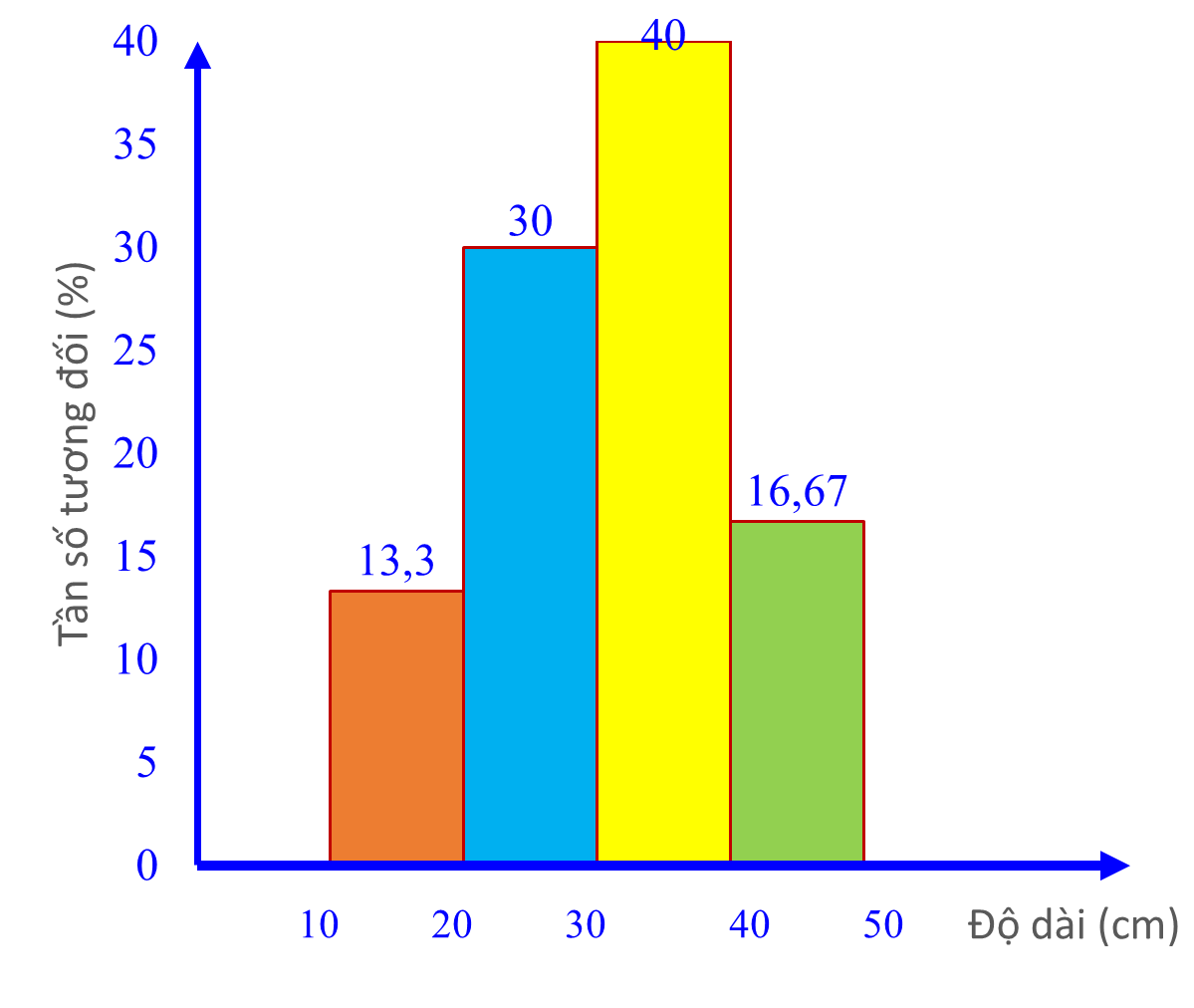
a) (0,5 điểm) Tần số tương đối của các nhóm lần lượt là: \({f_1} = \frac{{8.100}}{{60}}\% = 13,33\% ;{f_2} = \frac{{18.100}}{{60}}\% = 30\% \)
\({f_3} = \frac{{24.100}}{{60}}\% = 40\% ;{f_4} = \frac{{10.100}}{{60}}\% = 16,67\% \)
b) (0,5 điểm) Bảng tần số tương đối ghép nhóm của mẫu số liệu ghép nhóm đó
|
Nhóm |
\(\left[ {10;20} \right)\) |
\(\left[ {20;30} \right)\) |
\(\left[ {30;40} \right)\) |
\[{\rm{[}}40;50]\] |
Cộng |
|
Tần số tương đối \(\left( \% \right)\) |
\[13,33\] |
\[30\] |
\[40\] |
\[16,67\] |
\(100\) |
c) (0,5 điểm)
Lời giải
Vì chỉ số của Zn và H ở hai bên phương trình phản ứng bằng nhau, nên ta chỉ quan tâm đến chỉ số của N và O
Theo định luật bảo toàn nguyên tố đối với N và O, ta có hệ phương trình:
\[\left\{ \begin{array}{l}4y = 2x + 2\\12y = 6x + 2 + 2y\end{array} \right.\] (0,25 điểm)
\[\left\{ \begin{array}{l}4y - 2x = 2\\10y - 6x = 2\end{array} \right.\]
\[\left\{ \begin{array}{l}2y - x = 1\,\,\,\,\,\,\,\,\left( 1 \right)\\5y - 3x = 1\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\]
Nhân \[2\] vế pt \[\left( 1 \right)\]với \[3\] ta được hệ pt: \[\left\{ \begin{array}{l}6y - 3x = 3\,\,\,\,\,\,\,\,\\5y - 3x = 1\,\,\,\,\,\,\end{array} \right.\]
Trừ từng vế \[2\] pt trên ta được \[y = 2\]
Thay \[y = 2\] vào pt \[\left( 1 \right)\]ta được \[x = 3\]
Vậy ta có phương trình sau cân bằng \[3Zn + 8HN{O_3} \to 3Zn{(N{O_3})_2} + 2NO + 4{H_2}O\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập