Trên bảng ta viết đa thức\(P(x) = a{x^2} + bx + c\)\((a \ne 0)\).

Ta viết lên bảng đa thức mới\({P_1}(x) = \frac{{P(x + 1) + P(x - 1)}}{2}\)rồi xoá đi đa thức \(P(x)\).

Ta viết lên bảng đa thức mới\({P_2}(x) = \frac{{{P_1}(x + 1) + {P_1}(x - 1)}}{2}\)rồi xoá đi đa thức \({P_1}(x)\).

Ta cứ tiếp tục làm như thế nhiều lần.

Chứng minh rằng nếu cứ tiếp tục làm như vậy nhiều lần thì đến một lúc nào đó ta nhận được một đa thức không có nghiệm.

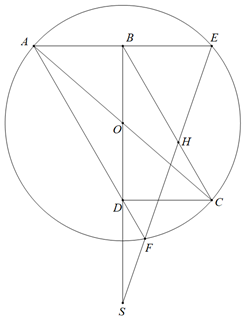
a) Đặt \(AB = a,BC = 2a\).Vì \(\widehat {ABC} = {120^0}\)\( \Rightarrow \)\(\widehat {BAD} = {60^0}\).

Áp dụng định lí cosin vào \(\Delta ABD\)ta có:

 \(\begin{array}{l}B{D^2} = A{B^2} + A{D^2} - 2.AB.AD.\cos BAD\\ = {a^2} + 4{a^2} - 2.2a.a.\cos 60\\ = 5{a^2} - 2{a^2} = 3{a^2} \Rightarrow B{D^2} + A{B^2} = A{D^2}\end{array}\)

 Do đó\(\Delta ABD\)là tam giác vuông theo định lí Pytago đảo.

b) Vì \(\Delta ABD\)là tam giác vuông nên \(OB \bot AE\)nên B là trung điểm của AE.

Mặt khác \(BH//AF\)nên theo tính chất đường trung bình ta có H là trung điểm của EF\$\Rightarrow$\(\widehat {OHF} = {90^0} = \widehat {OBE}\)$\Rightarrow$\(OBEH\)nội tiếp (ĐPCM).

c) Ta có: \(\widehat {CHS} = \widehat {BHE}.\)Vì OBEH nội tiếp nên \(\widehat {BHE} = \widehat {BOE} = \widehat {BOA} = \widehat {COS}\)

\( \Rightarrow \) OHCS nội tiếp.  

\( \Rightarrow \)\(\widehat {SCO} = \widehat {SHO} = {90^0}\).Từ đây ta có SC là tiếp tuyến của (O) (ĐPCM).