(1,5 điểm)

Một ngân hàng thống kê số tiền (đơn vị: triệu đồng) mà 80 hộ gia đình vay để phát triển sản xuất. Số liệu được ghi lại trong biểu đồ tần số ghép nhóm ở Hình 1.

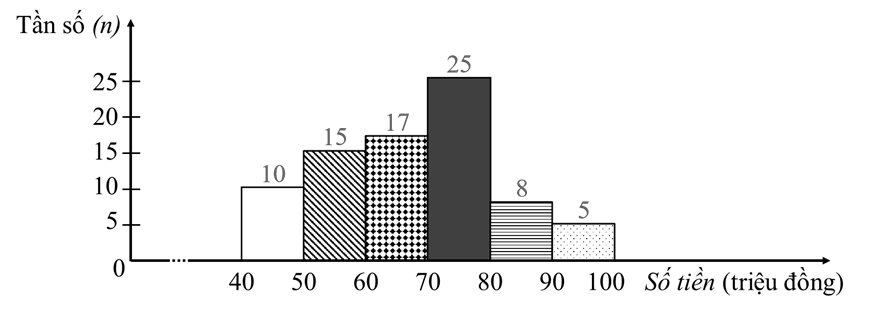
Hình 1

Lập bảng tần số tương đối ghép nhóm của mẫu số liệu được ghép nhóm đó.

Gọi số lần giảm giá \[100{\rm{ 000}}\]đồng/1tour để thu được doanh thu lớn nhất là \[x\] (lần)

Sau \[x\] lần giảm thì giá của một tour là: \[2{\rm{ }}000{\rm{ }}000 - 100{\rm{ }}000.x\] (đồng).

Vì cứ sau \[1\] lần giảm thì có thêm \[20\] người tham gia nên sau \[x\] lần giảm thì có thêm \[20.x\](người tham gia) nên tổng số người tham gia sau \[x\] lần giảm giá là:   \[200 + 20.x\] (người )

Tổng doanh thu sau \[x\] lần giảm giá là:

\[S = \left( {2{\rm{ }}000{\rm{ }}000 - 100{\rm{ }}000.x} \right).\left( {200 + 20.x} \right)\](đồng)

\[S = 100{\rm{ }}000.20.\left( {20 - x} \right).\left( {10 + x} \right)\](đồng)

\[S = 2{\rm{ 0}}00{\rm{ }}000.\left( { - {x^2} + 10x + 200} \right)\] (đồng)

Xét \[ - {x^2} + 10{\rm{x  +  200  = }} - {\rm{(}}{{\rm{x}}^2} - 10{\rm{x  + 25}} - 25 - 200)\] \[ =  - {{\rm{(x}} - 5)^2} + 225\]

Vì \[ - {{\rm{(x}} - 5)^2} + 225 \le 225\] nên \[2{\rm{ 0}}00{\rm{ }}000.\left( { - {x^2} + 10x + 200} \right) \le 2\,\,000\,\,000.225 = 450\,\,000\,\,000\]

hay\[S \le 450\,\,000\,\,000\]

\[{S_{m{\rm{ax}}}} = 450\,\,000\,\,000\]

Khi đó x = 5 (lần)

Vậy giá tour khi đó: \[2{\rm{ }}000{\rm{ }}000 - 100{\rm{ }}000.5 = 1{\rm{ 500 000}}\] (đồng).

a) Bán kính quả bóng bàn là: \[R = \frac{{40}}{2} = 20\,\,\left( {mm} \right) = 2\,\left( {cm} \right)\]

Thể tích quả bóng bàn là: \[V = \frac{4}{3}\pi {R^3} = \frac{4}{3} \cdot \pi  \cdot {2^3} = \frac{{32}}{3}\pi  \approx 33,51\,\,\left( {c{m^3}} \right)\]

b) Thể tích nước và phần chìm của quả bóng bàn trong cốc là: \[V = \pi {r^2}h = {3^2}.7,2\pi  = \frac{{324}}{5}\pi \,\,\left( {c{m^3}} \right)\]

Thể tích phần chìm của quả bóng bàn là: \[\frac{{324}}{5}\pi  - 200 \approx 3,58\,\,\left( {c{m^3}} \right)\]

Thể tích phần nổi của quả bóng bàn là: \[\frac{{32}}{3}\pi  - \left( {\frac{{324}}{5}\pi  - 200} \right) \approx 16,53\,\,\left( {c{m^3}} \right)\]

Tỉ lệ phần trăm thể tích phần nổi của quả bóng bàn trong thí nghiệm trên là: \[\frac{{16,53}}{{33,51}} \approx 49,33\,\% \]