(2 điểm)

a) Tính \(A = \sqrt 4  + \sqrt 8  + \sqrt {{{\left( {1 - \sqrt 2 } \right)}^2}}  - 3\sqrt 2 \).

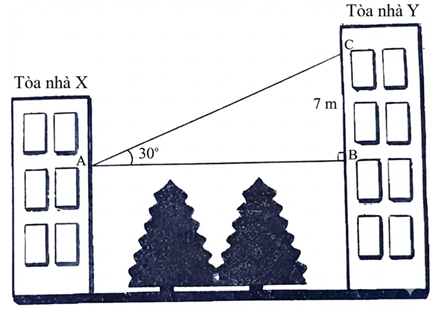
b) Để thực hành đo khoảng cách giữa hai tòa nhà \(X\) và \(Y\), một học sinh dùng giác kế tại vị trí \(A\) của tòa nhà và ngắm qua hai vị trí \(B,C\) của tòa nhà \(Y\) như hình vẽ. Khoảng cách giữa hai điểm \(B,C\) (ở hai tầng) bằng \(7\,{\rm{m}},\,\,\widehat {BAC} = 30^\circ ,\) vị trí \(A\) và \(B\) cùng độ cao so với mặt đất. Tính khoảng cách \(AB\) giữa hai tòa nhà đó (kết quả làm tròn đến chữ số thập phân thứ nhất của đơn vị mét).

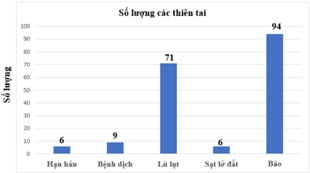
c) Hình bên là biểu đồ số lượng các thiên tai xảy ra tại Việt Nam giai doạn 1990-2021. Biểu đồ có bao nhiêu loại thiên tai và loại thiên tai nào xảy ra nhiểu nhất?

d) Lập bảng tấn sồ cho dữ liệu được biểu diễn trên biểu đồ sổ lượng các thiên tai ở hình bên.

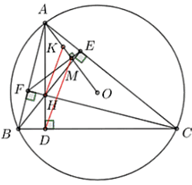
Do BE, CF là các đường cao nên \(\Delta BFC\) vuông tại F suy ra B, F, C cùng thuộc đường tròn đường kính BC và \(\Delta BEC\) vuông tại E nên \({\rm{B}},{\rm{E}},{\rm{C}}\)cùng thuộc đường tròn đường kính BC

Vậy B, C, E, F cùng thuộc đường tròn đường kính BC hay BFEC là tứ giác nội tiếp

Khi đó \(\widehat {BCE} + \widehat {BFE} = 180^\circ \) (tổng hai góc đổi của từ giác nội tiếp)

Mà \(\widehat {BFE} + \widehat {AFE} = 180^\circ \) (hai góc kè bù) nên \(\widehat {AFE} = \widehat {ACB}\).

b) Ta có \(\widehat {BOC} = 2\widehat {BAC} = 2 \cdot 60^\circ  = 120^\circ \) (cùng chắn cung BC)

Khi đó \({S_q} = \frac{{\pi  \cdot {R^2} \cdot 120}}{{360}} = \frac{{\pi  \cdot {3^2} \cdot 120}}{{360}} \approx 9,42\,\,\left( {{\rm{c}}{{\rm{m}}^2}} \right)\)

c) Ta có \(\Delta OAB\) cân tại \(O\) nên:

\[\widehat {OAB} = \widehat {OBA} = \frac{{180^\circ  - \widehat {AOB}}}{2} = 90^\circ  - \frac{{\widehat {AOB}}}{2} = 90^\circ  - \widehat {ACB}.\]

Lại có BFEC nội tiếp nên \(\widehat {AEF} = \widehat {BCA}\) (cùng bù \(\widehat {BFE}\))

Suy ra \(\widehat {OAB} + \widehat {AFE} = 90^\circ  - \widehat {ACB} + \widehat {ACB} = 90^\circ \) hay \(\Delta AMF\) vuông tại M

Suy ra \(AO \bot EF\)

Mà \(AK \bot EF\) tại \(M\) nên \(A,K,M,O\) thẳng hàng

Xét \(\Delta AEF\) và \(\Delta ABC\) có

\(\widehat {BAC}\) chung

\(\widehat {AFE} = \widehat {ACB}\)

Do đó 

Mà \(K,\,\,H\) tương ứng là trực tâm của \(\Delta AEF,\,\,\Delta ABC\).

Và \(AM,\,\,AD\) tương ứng là các đường cao hạ từ \(A\) xuống \(EF,\,\,BC.\)

Do đó \(\frac{{AK}}{{AH}} = \frac{{AM}}{{AD}}\) hay \(\frac{{AK}}{{AM}} = \frac{{AH}}{{AD}}\)

Từ đó suy ra \(HK\,{\rm{//}}\,MD\) (theo định lí Thales đảo)

Nửa chu vi bế bơi là \(36:2 = 18\left( {\rm{m}} \right)\)

   Gọi chiều dài của bể bơi lần lượt là \(x\left( {\rm{m}} \right)\,\,\left( {0 < x < 18} \right).\)

   Chiều rộng của bế bơi là \(18 - x\left( {\rm{m}} \right)\)

   Diện tích bế bơi là \(x\left( {18 - x} \right)\left( {{{\rm{m}}^2}} \right)\)

   Vì diện tích hình chữ nhật là \(80\,\,{{\rm{m}}^2}\) nên ta có phương trình \(x\left( {18 - x} \right) = 80\) \( - {x^2} + 18x - 80 = 0\)

\( - {x^2} + 18x - 80 = 0\)

\({x^2} - 18x + 80 = 0\)

\({x^2} - 10x - 8x + 80 = 0\)

\(x\left( {x - 10} \right) - 8\left( {x - 10} \right) = 0\)

\(\left( {x - 10} \right)\left( {x - 8} \right) = 0\)

\(x = 8\) hoặc \(x = 10\)

Vì chiều dài lớn hơn chiều rộng nên chiều dài bể bơi là 10 m, chiều rộng bể bơi là 8 m.

   Diện tích phần gạch lát là: \(12.10 - 80 = 40\left( {{{\rm{m}}^2}} \right)\)