(1,5 điểm) Cho hai biểu thức A = và B = với x > 0, x khác 1
Tính giá trị của biểu thức \(A\) khi \(x = 36\)
Tính giá trị của biểu thức \(A\) khi \(x = 36\)
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 7 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Thay \(x = 36\)(tmđk) vào \(A\) ta được \(A = \frac{{36 - 5}}{{\sqrt {36} }} = \frac{{31}}{6}\)
Vậy \(A = \frac{{31}}{6}\)khi \(x = 36\)
Câu hỏi cùng đoạn
Câu 2:
Rút gọn biểu thức \[B\].
Giải bởi Vietjack
\(B = \frac{{2x + 2\sqrt x }}{{x - 1}} - \frac{{\sqrt x }}{{\sqrt x - 1}}\) với \(x > 0,x \ne 1\).
\[B = \frac{{2x + 2\sqrt x }}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} - \frac{{\sqrt x \left( {\sqrt x + 1} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\]
\[B = \frac{{x + \sqrt x }}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} = \frac{{\sqrt x \left( {\sqrt x + 1} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\]
\[B = \frac{{\sqrt x }}{{\sqrt x - 1}}\]
Vậy \[B = \frac{{\sqrt x }}{{\sqrt x - 1}}\] , \(x > 0,x \ne 1\)
Câu 3:
Tìm tất cả giá trị nguyên của \(x\) để biểu thức \(P = AB\) có giá trị nguyên.
Giải bởi Vietjack
Tìm tất cả giá trị nguyên của \(x\) để biểu thức \(P = AB\) có giá trị nguyên
\[P = \frac{{x - 5}}{{\sqrt x - 1}}\]
\[P = \frac{{x - 5}}{{\sqrt x - 1}} = 0 \Rightarrow x = 5\,\left( {tm} \right)\]
\[P \ne 0,x \in Z,\sqrt x \in I \Rightarrow P \notin Z\]
\[P = \sqrt x + 1 - \frac{4}{{\sqrt x - 1}} \ne 0,x \in Z,\sqrt x \in Z \Rightarrow \sqrt x - 1 \in U\left( 4 \right)\]
\[x \in \left\{ {4;9;25} \right\}\] (tmđk)
Vậy \[x \in \left\{ {4;5;9;25} \right\}\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
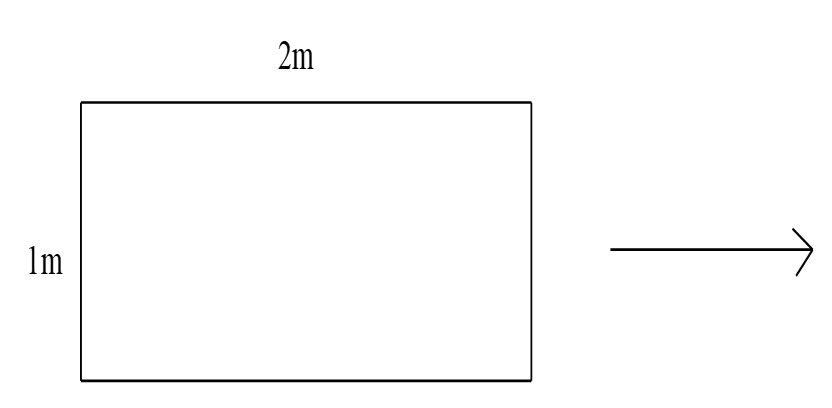
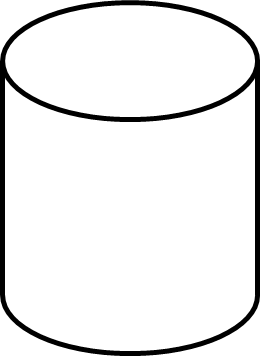
Gọi \(R\) là bán kính đáy của hình trụ
Ta có : \(C = 2\pi R \Leftrightarrow R = \frac{C}{{2\pi }} = \frac{2}{{2\pi }} = \frac{1}{\pi }\) \((m)\)
Thể tích của hình trụ là : \(V = \pi {R^2}h = \pi .{\left( {\frac{1}{\pi }} \right)^2}.1 = \pi .\frac{1}{{{\pi ^2}}} = \frac{1}{\pi } = \frac{1}{{3,14}} \approx 0,32{m^3}\)
Vậy thùng đựng được \(0,32{m^3}\) nước.
b) Để lấy bóng, em bé chỉ cần đổ đầy nước vào thùng tôn. Em bé cần lấy ít nhất \(0,32{m^3}\) nước.
Thì bóng nổi trên mặt thùng tôn khi đó sẽ an toàn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
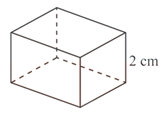
Gọi chiều rộng của đáy hộp là \(x\)( \(x > 0\), cm).
Ta có chiều dài của hộp là \(\frac{{500}}{{2x}}\) (cm)
Ta có diện tích toàn phần của chiếc hộp là
\(S = 2x \cdot \frac{{500}}{{2x}} + 2\left( {x + \frac{{500}}{{2x}}} \right) \cdot 2 = 500 + 2x + \frac{{250}}{x}\) (cm2)
Áp dụng bất đẳng thức Cauchy cho hai số thực dương \(2x\) và \(\frac{{250}}{x}\), ta có
\(2x + \frac{{250}}{x} \ge 2\sqrt {2x \cdot \frac{{250}}{x}} = 20\sqrt 5 \)
Từ đó \(S \ge 500 + 20\sqrt 5 \,\,\) (cm2)
Dấu xảy ra khi và chỉ khi \(2x = \frac{{250}}{x}\) hay \({x^2} = \frac{{250}}{2} = 125\)
Suy ra \(x = 5\sqrt 5 \)cm, từ đó \(\frac{{250}}{{5\sqrt 5 }} = 10\sqrt 5 \)cm.
Vậy chiều rộng của hộp là \(5\sqrt 5 \)cm, chiều dài là \(10\sqrt 5 \)cm.
Chứng minh bổ sung Bất đẳng thức Cauchy
Xét hai số thực dương \(a\), \(b\)ta có \(\frac{{a + b}}{2} \ge \sqrt {ab} \).
Thật vậy, vì \(a\), \(b\) là các số thực dương nên
Từ \(\frac{{a + b}}{2} \ge \sqrt {ab} \), suy ra \(a + b \ge 2\sqrt {ab} \)
Hay \({\left( {\sqrt a } \right)^2} + {\left( {\sqrt b } \right)^2} - 2\sqrt {ab} \ge 0\)
\({\left( {\sqrt a - \sqrt b } \right)^2} \ge 0\) (luôn đúng)
Vậy với hai số thực dương \(a\), \(b\) bất kỳ ta có \(\frac{{a + b}}{2} \ge \sqrt {ab} \).
Dấu “\( = \)” xảy ra khi \(a = b\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập