Trong các kì thi tuyển sinh vào lớp 10 THPT, cả hai trường A và B có tổng số 380 thí sinh dự thi. Sau khi có kết quả, số thí sinh trúng tuyển của cả hai trường là 191 thí sinh. Theo thống kê thì trường A có tỉ lệ trúng tuyển là 55% tổng số thí sinh dự thi của trường A, trường B có tỉ lệ trúng tuyển là 45% tổng số thí sinh dự thi của trường B. Hỏi mỗi trường có bao nhiêu thí sinh dự thi?

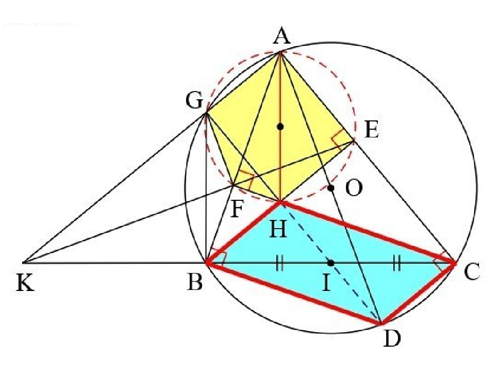
1) Ta có: \(\widehat {BEC} = \widehat {BFC} = {90^^\circ }\) nên \({\rm{B}},{\rm{F}},{\rm{E}},{\rm{C}}\) cùng thuộc đường tròn đường kính \({\rm{BC}}\).

Suy ra tứ giác \({\rm{BFEC}}\) nội tiếp đường tròn đường kính \({\rm{BC}}\).

2) Xét \(\Delta KBF\) và \(\Delta KEC\) có:

\(\widehat {{\rm{KFB}}} = \widehat {{\rm{KCE}}}\) (vì cùng bù với góc \({\rm{BFE}})\)

\(\widehat {{\rm{BKF}}}\) : chung

Do đó:

Suy ra: \(\frac{{{\rm{KB}}}}{{{\rm{KE}}}} = \frac{{{\rm{KF}}}}{{{\rm{KC}}}} \Rightarrow {\rm{KB}}{\rm{.KC}} = {\rm{KF}}.{\rm{KE}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\)        (1)

3) Ta chứng minh được (g.g)

Suy ra:\(\frac{{{\rm{KB}}}}{{{\rm{KA}}}} = \frac{{{\rm{KG}}}}{{{\rm{KC}}}} \Rightarrow {\rm{KB}}{\rm{.KC}} = {\rm{KA}}{\rm{.KG}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\)                (2)

Từ (1), (2) suy ra: \({\rm{KA}}{\rm{.KG}} = {\rm{KE}}{\rm{.KF}}\,\,\,\,\,\,\,\,\,\,\,\)

Xét \(\Delta {\rm{KGF}}\) và \(\Delta {\rm{KEA}}\) có: \(\frac{{{\rm{KG}}}}{{{\rm{KE}}}} = \frac{{{\rm{KF}}}}{{{\rm{KA}}}}\) (vì \({\rm{KA}}{\rm{.KG}} = {\rm{KE}}{\rm{.KF}}\)); \(\widehat {{\rm{GKF}}}\) : chung

Do đó: (c.g.c)

Suy ra: \(\widehat {{\rm{KGF}}} = \widehat {{\rm{KEA}}} \Rightarrow \) Tứ giác AGFE nội tiếp                              (3)

Tứ giác \({\rm{AEHF}}\) nội tiếp (vì \(\widehat {{\rm{AEH}}} + \widehat {{\rm{AFH}}} = {180^^\circ }\))                             (4)

Từ (3) và (4) suy ra 5 điểm: A, G, F, H, E cùng thuộc đường tròn đường kính \({\rm{AH}}\).

4) Kẻ đường kính \({\rm{AD}}\) của đường tròn \(({\rm{O}})\). Khi đó: \({\rm{BH}}//{\rm{CD}}\) (vì cùng vuông góc với \({\rm{AC}}\)) \({\rm{CH}}//{\rm{BD}}\) (vì cùng vuông góc với \({\rm{AB}}\)). Do đó tứ giác \({\rm{BHCD}}\) là hình bình hành.

Lại có \({\rm{I}}\) là trung điểm của đường chéo \({\rm{BC}}\) nên I là trung điểm của đường chéo \({\rm{HD}}\)

Suy ra: H, I, D thẳng hàng                                                                 (5)

Ta có: \(\widehat {{\rm{AGD}}} = {90^^\circ }\) (vì nội tiếp chắn nửa đường tròn)                       (6)

\(\widehat {AGH} = \widehat {AFH} = {90^^\circ }\) (vì nội tiếp cùng chắn cung \({\rm{AH}}\))                      (7)

Từ (5), (6) và (7) suy ra: \({\rm{H}},{\rm{G}},{\rm{I}}\) thẳng hàng. Vậy \({\rm{HI}}\) vuông góc với \({\rm{AK}}\).

1. Phương trình có \(\Delta  = {({\rm{m}} + 3)^2} - 4 \cdot \left( {\frac{1}{4}\;{{\rm{m}}^2} + 1} \right) = {{\rm{m}}^2} + 6\;{\rm{m}} + 9 - {{\rm{m}}^2} - 4 = 6\;{\rm{m}} + 5\)

Phương trình có hai nghiệm phân biệt \({{\rm{x}}_1},{{\rm{x}}_2} \Leftrightarrow 6\;{\rm{m}} + 5 > 0 \Leftrightarrow {\rm{m}} > \frac{{ - 5}}{6}\)

Theo hệ thức Vi - ét ta có: \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = m + 3}\\{{x_1} \cdot {x_2} = \frac{1}{4}{m^2} + 1}\end{array}} \right.\)

Theo đề ta có: \(2{\left( {{{\rm{x}}_1} + {{\rm{x}}_2}} \right)^2} - 8{{\rm{x}}_1}{{\rm{x}}_2} = 34\)

\( \Leftrightarrow 2.{({\rm{m}} + 3)^2} - 8.\left( {\frac{1}{4}\;{{\rm{m}}^2} + 1} \right) = 34 \Leftrightarrow 2\;{{\rm{m}}^2} + 12\;{\rm{m}} + 18 - 2\;{{\rm{m}}^2} - 8 - 34 = 0\)

\( \Leftrightarrow 12\;{\rm{m}} - 24 = 0 \Leftrightarrow {\rm{m}} = 2\) (TMĐK). Vậy \({\rm{m}} = 2\) là giá trị cần tìm.

2. Vì \(A( - 1;5) \in (d):y = ax - 4\) nên: \(5 = {\rm{a}} \cdot ( - 1) - 4 \Leftrightarrow 5 =  - {\rm{a}} - 4 \Leftrightarrow {\rm{a}} =  - 9\)

Vậy a \( =  - 9\).

b) Tọa độ giao điểm của \(\left( {{{\rm{d}}_1}} \right)\) với trục hoành là \({\rm{A}}\left( {\frac{2}{3};0} \right)\)

Tọa độ giao điểm của \(\left( {{{\rm{d}}_1}} \right)\) với trục tung là \({\rm{B}}(0;2)\)

Ta có: \({\rm{OA}} = \left| {\frac{2}{3}} \right| = \frac{2}{3}(\) đvđd) \({\rm{OB}} = |2| = 2\)(đvđd)

\({\rm{AB}} = \sqrt {{\rm{O}}{{\rm{A}}^2} + {\rm{O}}{{\rm{B}}^2}}  = \sqrt {{{\left( {\frac{2}{3}} \right)}^2} + {2^2}}  = \frac{{2\sqrt {10} }}{3}({\rm{dvdd}})\)

Diện tích tam giác \({\rm{OAB}}\) là:

\({{\rm{S}}_{{\rm{OAB}}}} = \frac{1}{2} \cdot {\rm{OA}} \cdot {\rm{OB}} = \frac{1}{2} \cdot \frac{2}{3} \cdot 2 = \frac{2}{3}({\rm{dvdt}})\)

Khoảng cách từ gốc tọa độ \({\rm{O}}\) đến \(\left( {{{\rm{d}}_1}} \right)\) là:

\(\frac{{2.{{\rm{S}}_{{\rm{OAB}}}}}}{{{\rm{AB}}}} = \frac{{2 \cdot \frac{2}{3}}}{{\frac{{2\sqrt {10} }}{3}}} = \frac{{\sqrt {10} }}{5}\) (đvđd)