(2,5 điểm)
Một người mua hai loại hàng và phải trả tổng cộng \[21,7\] triệu đồng, kể cả thuế giá trị gia tăng (VAT) với mức \[10\,\% \] đối với loại hàng thứ nhất và \[8\,\% \] đối với loại hàng thứ hai. Nếu thuế VAT là \[9\,\% \] đối với cả hai loại hàng thì người đó phải trả tổng cộng \[21,8\] triệu đồng. Hỏi nếu không kể thuế VAT thì người đó phải trả bao nhiêu cho mỗi loại hàng ?
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 4 !!
Quảng cáo
Trả lời:
Giả sử không kể thuế VAT, người đó phải trả \(x\) triệu đồng cho loại hàng thứ nhất, \(y\) triệu đồng cho loại hàng thứ hai. \((x > 0;y > 0)\).
Khi đó số tiền phải trả cho loại hàng thứ nhất (kể cả thuế VAT \(10\% \) ) là \(\frac{{110}}{{100}}x\) (triệu đồng), cho loại hàng thứ hai với thuế VAT \(8\% \) là \(\frac{{108}}{{100}}y\) (triệu đồng).
Ta có phương trình \(\frac{{110}}{{100}}x + \frac{{108}}{{100}}y = 21,7\) hay \(1,1x + 1,08y = 21,7\).
Khi thuế VAT là \(9\% \) cho cả hai loại hàng thì số tiền phải trả là: \(\frac{{109}}{{100}}\left( {x + y\,} \right) = 21,8\) hay \(1,09x + 1,09y = 21,8{\rm{ }}\)
Ta có hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{1,1x + 1,08y = 21,7}\\{1,09x + 1,09y = 21,8{\rm{ }}}\end{array}} \right.\)
Chia cả hai vế phương trình \(\left( 2 \right)\) cho \(1,09\) ta được \(x + y = 20\)
Suy ra \(x = 20 - y\).
Thay \(x = 20 - y\) vào \(1,1x + 1,08y = 21,7\) phương trình ta được \(1,1\left( {20 - y} \right) + 1,08y = 21,7\) hay \( - 0,02y = - 0,3\) suy ra \(y = 15\).
Thay \(y = 15\) vào \(x = 20 - y\) ta được \(x = 20 - 15 = 5\).
Vậy với \(x = 5\), \(y = 15\) (thỏa mãn điều kiện).
Vậy loại thứ nhất \(5\) triệu đồng, loại thứ hai \(15\) triệu đồng.
Câu hỏi cùng đoạn
Câu 2:
Hưởng ứng ngày Chủ nhật xanh với chủ đề “Hãy hành động để môi trường thêm Xanh, Sạch, Đẹp”, một trường THCS đã cử học sinh của hai lớp 9A và 9B cùng tham gia làm tổng vệ sinh một con đường, sau \(\frac{{35}}{{12}}\) giờ thì làm xong công việc. Nếu làm riêng từng lớp thì thời gian học sinh lớp 9A làm xong công việc ít hơn thời gian học sinh lớp 9B là \(2\) giờ. Hỏi nếu mỗi lớp làm một mình thì sau bao nhiêu giờ sẽ làm xong công việc?
Giả sử không kể thuế VAT, người đó phải trả \(x\) triệu đồng cho loại hàng thứ nhất, \(y\) triệu đồng cho loại hàng thứ hai. \((x > 0;y > 0)\).
Khi đó số tiền phải trả cho loại hàng thứ nhất (kể cả thuế VAT \(10\% \) ) là \(\frac{{110}}{{100}}x\) (triệu đồng), cho loại hàng thứ hai với thuế VAT \(8\% \) là \(\frac{{108}}{{100}}y\) (triệu đồng).
Ta có phương trình \(\frac{{110}}{{100}}x + \frac{{108}}{{100}}y = 21,7\) hay \(1,1x + 1,08y = 21,7\).
Khi thuế VAT là \(9\% \) cho cả hai loại hàng thì số tiền phải trả là: \(\frac{{109}}{{100}}\left( {x + y\,} \right) = 21,8\) hay \(1,09x + 1,09y = 21,8{\rm{ }}\)
Ta có hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{1,1x + 1,08y = 21,7}\\{1,09x + 1,09y = 21,8{\rm{ }}}\end{array}} \right.\)
Chia cả hai vế phương trình \(\left( 2 \right)\) cho \(1,09\) ta được \(x + y = 20\)
Suy ra \(x = 20 - y\).
Thay \(x = 20 - y\) vào \(1,1x + 1,08y = 21,7\) phương trình ta được \(1,1\left( {20 - y} \right) + 1,08y = 21,7\) hay \( - 0,02y = - 0,3\) suy ra \(y = 15\).
Thay \(y = 15\) vào \(x = 20 - y\) ta được \(x = 20 - 15 = 5\).
Vậy với \(x = 5\), \(y = 15\) (thỏa mãn điều kiện).
Vậy loại thứ nhất \(5\) triệu đồng, loại thứ hai \(15\) triệu đồng.
Câu 3:
Phương trình \({x^2} + mx + 2m - 4 = 0\) có\({x_1},\;{x_2}\) hai nghiệm và \({x_1} = - 1\), tính giá trị của biểu thức \(N = \frac{1}{{{x_1} + 3}} + \frac{1}{{{x_2} + 3}}\)
Thay \({x_1} = - 1\) vào phương trình đã cho ta có
\({\left( { - 1} \right)^2} + m\,.\,\left( { - 1} \right) + 2m - 4 = 0\)
\(m = 3\)
Ta có \(N = \frac{1}{{{x_1} + 3}} + \frac{1}{{{x_2} + 3}} = \frac{{{x_1} + {x_2} + 6}}{{\left( {{x_1} + 3} \right)\left( {{x_2} + 3} \right)}}\) ( điều kiện \({x_1} \ne - 3\), \({x_2} \ne - 3\))
\(N = \frac{{{x_1} + {x_2} + 6}}{{{x_1}{x_2} + 3\left( {{x_1} + {x_2}} \right) + 9}}\)
\(N = \frac{{ - m + 6}}{{2m - 4 + 3\left( { - m} \right) + 9}}\)\( = \frac{{6 - m}}{{5 - m}}\)\( = \frac{{6 - 3}}{{5 - 3}}\)\( = \frac{3}{2}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
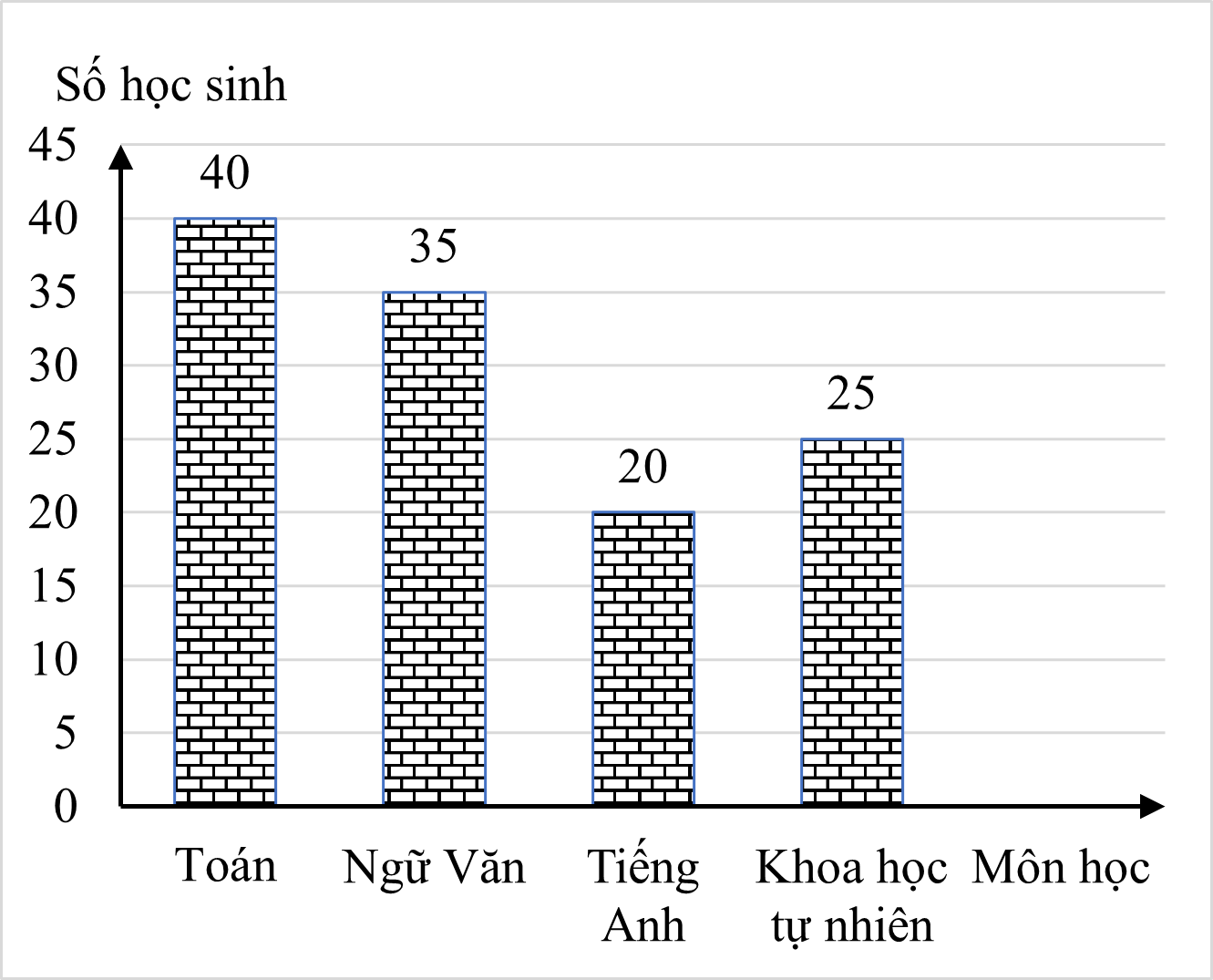
Quan sát biểu đồ, ta có:
Tổng số học sinh khối \(9\) là: \(40 + 35 + 20 + 25 = 120\) học sinh. Vậy \(N = 120\).
Bảng tần số:
|
Môn học \(\left( x \right)\) |
Toán |
Ngữ Văn |
Tiếng Anh |
Khoa học tự nhiên |
Cộng |
|
Tần số \(\left( n \right)\) |
\(40\) |
\(35\) |
\(20\) |
\(25\) |
\(N = 120\) |
Tần số tương đối của số học sinh yêu thích các môn Toán, Ngữ Văn, Tiếng Anh, Khoa học tự nhiên lần lượt là:
\({f_1} = \frac{{40}}{{120}}\,\, \cdot \,\,100\% \approx 33,33\% \); \({f_2} = \frac{{35}}{{120}}\,\, \cdot \,\,100\% \approx 29,17\% \);
\({f_3} = \frac{{20}}{{120}}\,\, \cdot \,\,100\% \approx 16,67\% \); \({f_4} = \frac{{25}}{{120}}\,\, \cdot \,\,100\% \approx 20,83\% \).
Bảng tần số tương đối:
|
Môn học \(\left( x \right)\) |
Toán |
Ngữ Văn |
Tiếng Anh |
Khoa học tự nhiên |
Cộng |
|
Tần số tương đối \(\left( \% \right)\) |
\(33,33\) |
\(29,17\) |
\(16,67\) |
\(20,83\) |
\(100\) |
Lời giải
Đổi \[40\,mm = 4\,cm\]
a) Bán kính của quả bóng bàn là: \(4:2 = 2\,(cm)\)
Thể tích của quả bóng bàn là:
\[{V_1} = \frac{4}{3}\pi {R^3}\]\[ = \frac{4}{3} \cdot {3,14.2^3}\]\[ = 33,49\,\,\left( {{\rm{c}}{{\rm{m}}^3}} \right)\]
b) Thể tích nước dâng: \[{V_2} = \pi {R^2}.h\]\[ = {3,14.3^2}.7,2\]\[ = 203,472\,\,\left( {{\rm{c}}{{\rm{m}}^3}} \right)\]
Thể tích phần bóng chìm: \({V_3} = 203,472 - 200 = 3,472\,({\rm{c}}{{\rm{m}}^3})\)
Vậy thể tích phần nổi quả bóng:
\[V = {V_1} - {V_3}\]\[ = 33,49 - 3,472\]\[ \approx 30,02\,\,\left( {{\rm{c}}{{\rm{m}}^3}} \right)\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.