(0,5 điểm) Một mảnh vải hình vuông có độ dài cạnh là \(c\) (với \(c < 1\)). Lấy một cạnh mảnh vài hình vuông cố định, người ta cắt mảnh vải đó thành một mảnh vải hình tam giác vơi độ dài ba cạnh lần lượt \(a\), \(b\), \(c\) thỏa mãn \(a + b + c = 1\) và biểu thức \(P = \frac{{a + b}}{{abc}}\) có giá trị nhỏ nhất. Hãy xác định kích thước của mảnh vài hình tam giác đó.
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 4 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Vì mảnh vải hình tam giác có độ dài ba cạnh lần lượt \(a\), \(b\), \(c\) thỏa mãn \(a + b + c = 1\) nên \(0 < a < 1\); \(0 < b < 1\); \(0 < c < 1\)
Ta có \({a^2} + {b^2} \ge 2ab\),
Suy ra \({\left( {a + b} \right)^2} \ge 4ab\) hay \(ab \le \frac{{{{\left( {a + b} \right)}^2}}}{4}\),
Suy ra \(\frac{1}{{ab}} \ge \frac{4}{{{{\left( {a + b} \right)}^2}}}\)
Dấu bằng xảy ra khi \(a = b\)
Khi đó ta có \(P = \frac{{a + b}}{{abc}} = \frac{{a + b}}{c}\, \cdot \,\frac{1}{{ab}} \ge \frac{{a + b}}{c}\, \cdot \,\frac{4}{{{{\left( {a + b} \right)}^2}}} = \frac{4}{{c\left( {a + b} \right)}}\)
Áp dụng bất đẳng thức Cauchy, ta có \(\left( {a + b} \right) + c \ge 2\sqrt {\left( {a + b} \right)\,.\,c} \),
Suy ra \(1 \ge 2\sqrt {\left( {a + b} \right)\,.\,c} \)
Do đó \(\sqrt {\left( {a + b} \right)\,.\,c} \le \frac{1}{2}\),
Suy ra \(\left( {a + b} \right)\,.\,c \le \frac{1}{4}\)
Suy ra \(\frac{4}{{\left( {a + b} \right)\,.\,c}} \ge 16\) hay \(P \ge 16\)
Dấu bằng xảy ra khi \(\left\{ \begin{array}{l}a = b\\a + b = c\\a + b + c = 1\end{array} \right.\), suy ra \(\left\{ \begin{array}{l}a = b = \frac{1}{4}\\c = \frac{1}{2}\end{array} \right.\) ( thỏa mãn các điều kiện)
Do đó min \(P = 16\) khi \(\left\{ \begin{array}{l}a = b = \frac{1}{4}\\c = \frac{1}{2}\end{array} \right.\)
Vậy kích thước của mảnh vài hình tam giác đó là \(a = b = \frac{1}{4}\); \(c = \frac{1}{2}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đổi \[40\,mm = 4\,cm\]
a) Bán kính của quả bóng bàn là: \(4:2 = 2\,(cm)\)
Thể tích của quả bóng bàn là:
\[{V_1} = \frac{4}{3}\pi {R^3}\]\[ = \frac{4}{3} \cdot {3,14.2^3}\]\[ = 33,49\,\,\left( {{\rm{c}}{{\rm{m}}^3}} \right)\]
b) Thể tích nước dâng: \[{V_2} = \pi {R^2}.h\]\[ = {3,14.3^2}.7,2\]\[ = 203,472\,\,\left( {{\rm{c}}{{\rm{m}}^3}} \right)\]
Thể tích phần bóng chìm: \({V_3} = 203,472 - 200 = 3,472\,({\rm{c}}{{\rm{m}}^3})\)
Vậy thể tích phần nổi quả bóng:
\[V = {V_1} - {V_3}\]\[ = 33,49 - 3,472\]\[ \approx 30,02\,\,\left( {{\rm{c}}{{\rm{m}}^3}} \right)\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
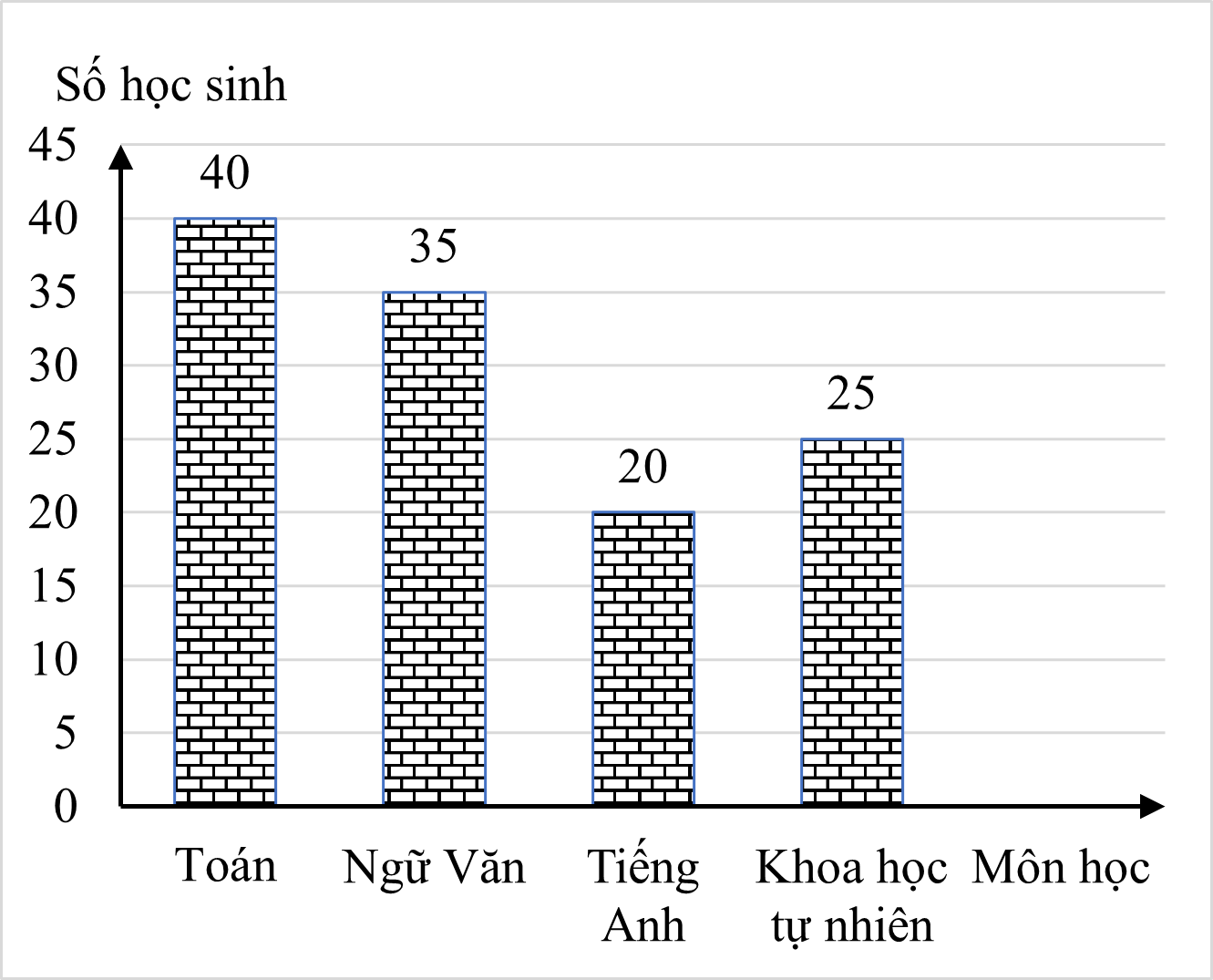
Quan sát biểu đồ, ta có:
Tổng số học sinh khối \(9\) là: \(40 + 35 + 20 + 25 = 120\) học sinh. Vậy \(N = 120\).
Bảng tần số:
|
Môn học \(\left( x \right)\) |
Toán |
Ngữ Văn |
Tiếng Anh |
Khoa học tự nhiên |
Cộng |
|
Tần số \(\left( n \right)\) |
\(40\) |
\(35\) |
\(20\) |
\(25\) |
\(N = 120\) |
Tần số tương đối của số học sinh yêu thích các môn Toán, Ngữ Văn, Tiếng Anh, Khoa học tự nhiên lần lượt là:
\({f_1} = \frac{{40}}{{120}}\,\, \cdot \,\,100\% \approx 33,33\% \); \({f_2} = \frac{{35}}{{120}}\,\, \cdot \,\,100\% \approx 29,17\% \);
\({f_3} = \frac{{20}}{{120}}\,\, \cdot \,\,100\% \approx 16,67\% \); \({f_4} = \frac{{25}}{{120}}\,\, \cdot \,\,100\% \approx 20,83\% \).
Bảng tần số tương đối:
|
Môn học \(\left( x \right)\) |
Toán |
Ngữ Văn |
Tiếng Anh |
Khoa học tự nhiên |
Cộng |
|
Tần số tương đối \(\left( \% \right)\) |
\(33,33\) |
\(29,17\) |
\(16,67\) |
\(20,83\) |
\(100\) |
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập