(1,5 điểm)
Khảo sát thời gian tập thể dục của một số học sinh lớp \[9\] thu được mẫu số liệu ghép nhóm sau:
Thời gian (phút)
\[\left[ {0\,\,;\,\,20} \right)\]
\[\left[ {20\,\,;\,\,40} \right)\]
\[\left[ {40\,\,;\,\,60} \right)\]
\[\left[ {60\,\,;\,\,80} \right)\]
Số học sinh
\[8\]
\[9\]
\[11\]
\[8\]
Tính tần số tương đối của nhóm \[\left[ {40\,\,;\,\,60} \right)\]? (Làm tròn đến hàng phần mười)
Khảo sát thời gian tập thể dục của một số học sinh lớp \[9\] thu được mẫu số liệu ghép nhóm sau:
|
Thời gian (phút) |
\[\left[ {0\,\,;\,\,20} \right)\] |
\[\left[ {20\,\,;\,\,40} \right)\] |
\[\left[ {40\,\,;\,\,60} \right)\] |
\[\left[ {60\,\,;\,\,80} \right)\] |
|
Số học sinh |
\[8\] |
\[9\] |
\[11\] |
\[8\] |
Tính tần số tương đối của nhóm \[\left[ {40\,\,;\,\,60} \right)\]? (Làm tròn đến hàng phần mười)
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 48 !!
Quảng cáo
Trả lời:
Nhóm \[\left[ {40\,\,;\,\,60} \right)\] có tần số tương đối là \[\frac{{11}}{{36}} \approx 30,6\% \]
Câu hỏi cùng đoạn
Câu 2:
Hình dưới đây mô tả một đĩa tròn, cân đối bằng bìa cứng được chia làm tám phần bằng nhau và ghi các số \[1\,;\,\,2\,;\,\,3\,;\,\,4\,;\,\,5\,;\,\,6\,;\,\,7\,;\,\,8\]. Chiếc kim được gắn cố định vào trục quay ở tâm của đĩa. Quay đĩa tròn một lần.
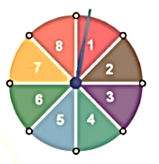
Tính xác suất của các biến cố sau: “Mũi tên chỉ vào hình quạt ghi số là ước của \[8\]”.

Tính xác suất của các biến cố sau: “Mũi tên chỉ vào hình quạt ghi số là ước của \[8\]”.
Ta có\(\Omega = \left\{ {1\,;\,2\,;\,3\,;\,4\,;\,5\,;\,6\,;\,7\,;\,\left. 8 \right\}} \right.\), có 8 phần tử.
Các kết quả thuận lợi cho biến cố: “Mũi tên chỉ vào hình quạt ghi số là ước của \[8\]”
là: \[1\,;\,2\,;\,4\,;\,8\]
\( \Rightarrow \)Xác suất của biến cố: “Mũi tên chỉ vào hình quạt ghi số là ước của \[8\]” là: \(\frac{4}{8} = \frac{1}{2}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
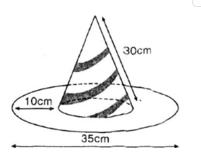
a) Bán kính đường tròn đáy của hình nón: \[r = \frac{{35 - 2.10}}{2} = 7,5\,({\rm{cm}})\]
Chiều cao của cái mũ: \[h = \sqrt {{{30}^2} - {{7,5}^2}} \approx 29(cm)\]
Tính thể tích của cái mũ: \[V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {.7,5^2}.29 = 543,75\pi \approx 1708(c{m^3})\]
b) Diện tích giấy làm nên cái mũ là tổng diện tích xung quanh của hình nón và diện tích vành nón.
Diện tích xung quanh hình nón: \[Sxq\; = \pi .r.l = \pi .7,5.30 = 225\pi {\rm{ }}({\rm{c}}{{\rm{m}}^2})\]
Diện tích vành nón (hình vành khăn): \[{S_{vk}} = \pi .{\left( {\frac{{35}}{2}} \right)^2} - \pi {.7,5^2} = 250\pi \,({\rm{c}}{{\rm{m}}^2})\]
Diện tích tích giấy làm nên cái mũ : \[S = 225\pi + 250\pi = 475\pi {\rm{ }} \approx {\rm{ }}1492{\rm{ (c}}{{\rm{m}}^{\rm{2}}})\]
Lời giải

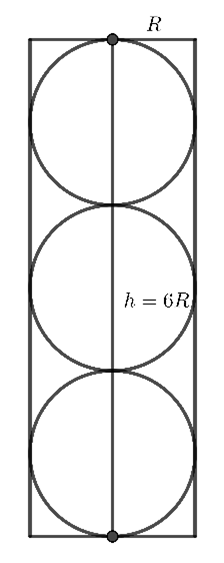
Đặt \(h,\,\,R\) lần lượt là đường cao và bán kính hình tròn đáy của hộp đựng bóng tennis.
Dễ thấy mỗi quả bóng tennis có cùng bán kính \(R\) với hình tròn đáy của hộp đựng bóng tennis và \(h = 6R\).
Do đó ta có:
Tổng thể tích của ba quả bóng là \({V_1} = 3.\frac{4}{3}\pi {R^3} = 4\pi {R^3}\);
Thể tích của hình trụ (hộp đựng bóng) là \({V_0} = \pi {R^2}h = 6\pi {R^3}\);
Thể tích phần còn trống của hộp đựng bóng là \({V_2} = {V_0} - {V_1} = 2\pi {R^3}\).
Khi đó tỉ lệ phần không gian còn trống so với hộp đựng bóng là \(\frac{{{V_2}}}{{{V_0}}} = \frac{1}{3} \approx 0,33 \approx 33\% \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.