(1,5 điểm)
Một cửa hàng sách thống kê số tiền (đơn vị: nghìn đồng) mà \[60\] khách hàng mua sách ở cửa hàng đó trong một ngày. Số liệu được ghi lại trong biểu đồ tần số ghép nhóm dưới đây.
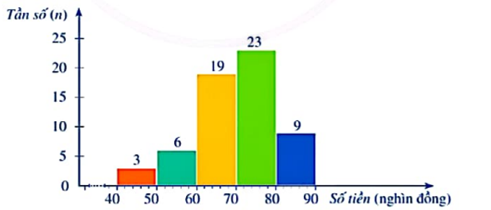
Tìm tần số ghép nhóm và tần số tương đối ghép nhóm của nhóm \[\left[ {40;50} \right)\]
(1,5 điểm)
Một cửa hàng sách thống kê số tiền (đơn vị: nghìn đồng) mà \[60\] khách hàng mua sách ở cửa hàng đó trong một ngày. Số liệu được ghi lại trong biểu đồ tần số ghép nhóm dưới đây.

Tìm tần số ghép nhóm và tần số tương đối ghép nhóm của nhóm \[\left[ {40;50} \right)\]
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 19 !!
Quảng cáo
Trả lời:
+ Tần số ghép nhóm của nhóm \[\left[ {40;50} \right)\] là \[3\].
+ Tần số tương đối ghép nhóm của nhóm \[\left[ {40;50} \right)\] là: \[\frac{3}{{60}}.100\% = 5\% \]
Câu hỏi cùng đoạn
Câu 2:
Một hộp có \[12\] tấm thẻ cùng loại, mỗi thẻ được ghi một trong các số \[1;2;3;...;12\]; hai thẻ khác nhau thì ghi hai số khác nhau. Xét phép thử “Rút ngẫu nhiên một thẻ trong hộp” và biến cố \[M\]: “Thẻ được rút ra ghi số chia hết cho \[3\]”. Tính xác suất của biến cố \[M\]?
+ Tập hợp các kết quả có thể xảy ra khi thực hiện phép thử “Rút ngẫu nhiên một thẻ trong hộp” là: \[\left\{ {1;2;3;...;12} \right\}\] ; có \[12\] kết quả
+ Các kết quả thuận lợi cho biến cố \[M\]: “thẻ được rút ra ghi số chia hết cho \[3\]” là: \[\left\{ {3;6;9;12} \right\}\]
+ Xác suất của biến cố \[M\]là: \[\frac{4}{{12}} = \frac{1}{3}\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
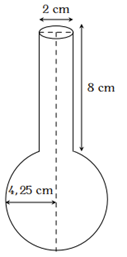
Bán kính đáy phần hình trụ là : \[2:1 = 2(cm)\]
Thể tích của phần bình hình trụ là : \[{V_1} = \pi .{r_1}^2.h = {3,14.1^2}.8 = 25,12(c{m^3})\]
Thể tích phần bình hình cầu là: \[{V_2} = \frac{4}{3}\pi .{r_2}^3 = \frac{4}{3}{.3,14.4,25^3} \approx 321,39(c{m^3})\]
Thể tích nước trong bình là : \[V = 25,12 + 321,39 = 346,51(c{m^3})\]
Vậy thể tích nước trong bình khoảng \[346,51(c{m^3})\]
Lời giải
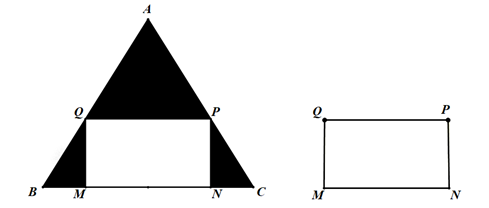
Gọi độ dài đoạn \[MB\] là \[x(cm)\], ta có:
Độ dài đoạn \[NC\] là \[x(cm)\]
Độ dài đoạn \[MN\] là \[20 - x - x = 20 - 2x(cm)\]
Tam giác \[BQM\] vuông tại \[M\] có:
\[\tan B = \tan {60^0} = \frac{{QM}}{{BM}} = \frac{{QM}}{x}\]
\[QM = x.\tan {60^0} = x.\sqrt 3 \]
Diện tích hình chữ nhật \[MNPQ\] là: \[S = MN.QM = (20 - 2x).x\sqrt 3 \]
Áp dụng bất đẳng thức Cauchy ta có: \[S = (20 - 2x).x\sqrt 3 = 2\sqrt 3 (10 - x).x \le 2\sqrt 3 {\left( {\frac{{10 - x + x}}{2}} \right)^2}\]
\[S \le 2\sqrt 3 .25 = 50\sqrt 3 \]
Dấu bằng xảy ra khi \[10 - x = x\] nên \[x = 5\]
Vậy \[MB = 5cm\] để hình chữ nhật \[MNPQ\] có diện tích lớn nhất.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.