(1,5 điểm) Cho hai biểu thức: \[A = \frac{3}{{\sqrt x - 2}} - \frac{{\sqrt x + 10}}{{x - 4}}\] và \[B = \frac{{\sqrt x + 2}}{{\sqrt x - 2}}\] với \[x \ge 0;x \ne 4\]
1) Tính giá trị của \[B\] tại \[x = 9\]
2) Rút gọn \[A\]
3) Đặt \[P = A.B\]. Tìm số nguyên tố \[x\] để \[P \le - 1\]
(1,5 điểm) Cho hai biểu thức: \[A = \frac{3}{{\sqrt x - 2}} - \frac{{\sqrt x + 10}}{{x - 4}}\] và \[B = \frac{{\sqrt x + 2}}{{\sqrt x - 2}}\] với \[x \ge 0;x \ne 4\]
1) Tính giá trị của \[B\] tại \[x = 9\]
2) Rút gọn \[A\]
3) Đặt \[P = A.B\]. Tìm số nguyên tố \[x\] để \[P \le - 1\]
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 19 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
1) Thay \[x = 9\] (thỏa mãn điều kiện) vào biểu thức \[B\] ta có:
\[B = \frac{{\sqrt 9 + 2}}{{\sqrt 9 - 2}} = \frac{{3 + 2}}{1} = 5\]
Vậy giá trị của \[B\] tại \[x = 9\] là \[5\].
2) \[A = \frac{3}{{\sqrt x - 2}} - \frac{{\sqrt x + 10}}{{x - 4}}\]
\[A = \frac{{3\left( {\sqrt x + 2} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}} - \frac{{\sqrt x + 10}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\]
\[A = \frac{{3\left( {\sqrt x + 2} \right) - \sqrt x - 10}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\]
\[A = \frac{{2\sqrt x - 4}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}} = \frac{{2\left( {\sqrt x - 2} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\]
\[A = \frac{2}{{\sqrt x + 2}}\]
3) \[P = A.B = \frac{2}{{\sqrt x + 2}}.\frac{{\sqrt x + 2}}{{\sqrt x - 2}} = \frac{2}{{\sqrt x - 2}}\]
\[P \le - 1 \Leftrightarrow \frac{2}{{\sqrt x - 2}} \le - 1 \Leftrightarrow \frac{2}{{\sqrt x - 2}} + 1 \le 0 \Leftrightarrow \frac{{\sqrt x }}{{\sqrt x - 2}} \le 0\]
* Nếu \[\frac{{\sqrt x }}{{\sqrt x - 2}} = 0\] thì \[\sqrt x = 0 \Leftrightarrow x = 0\] (không thỏa mãn đk x là số nguyên tố)
* Nếu \[\frac{{\sqrt x }}{{\sqrt x - 2}} < 0\] thì ta có hai trường hợp sau:
\[TH1:\left\{ \begin{array}{l}\sqrt x > 0\\\sqrt x - 2 < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > 0\\x < 4\end{array} \right. \Leftrightarrow 0 < x < 4\](thỏa mãn đk \[x \ge 0;x \ne 4\]) mà \[x\] là số nguyên tố nên \[x = 2;x = 3\]
\[TH2:\left\{ \begin{array}{l}\sqrt x < 0\\\sqrt x - 2 > 0\end{array} \right. \Leftrightarrow x \in \emptyset \]
Vậy \[x = 2;x = 3\] thì thỏa mãn đề bài
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
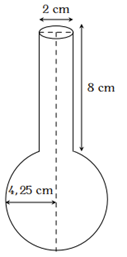
Bán kính đáy phần hình trụ là : \[2:1 = 2(cm)\]
Thể tích của phần bình hình trụ là : \[{V_1} = \pi .{r_1}^2.h = {3,14.1^2}.8 = 25,12(c{m^3})\]
Thể tích phần bình hình cầu là: \[{V_2} = \frac{4}{3}\pi .{r_2}^3 = \frac{4}{3}{.3,14.4,25^3} \approx 321,39(c{m^3})\]
Thể tích nước trong bình là : \[V = 25,12 + 321,39 = 346,51(c{m^3})\]
Vậy thể tích nước trong bình khoảng \[346,51(c{m^3})\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
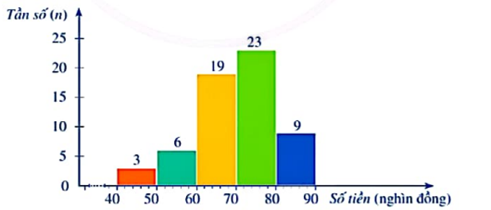
+ Tần số ghép nhóm của nhóm \[\left[ {40;50} \right)\] là \[3\].
+ Tần số tương đối ghép nhóm của nhóm \[\left[ {40;50} \right)\] là: \[\frac{3}{{60}}.100\% = 5\% \]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập