(2,5 điểm)
Bình muốn tạo ra \[500\] \[gam\] dung dịch \[HCl\] \[16\% \] từ hai loại dung dịch \[HCl\] \[10\% \] và \[HCl\] \[25\% \]. Hỏi Bình cần dùng bao nhiêu \[gam\]cho mỗi loại dung dịch đó?
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 19 !!
Quảng cáo
Trả lời:
Gọi khối lượng dung dịch \[HCl\] \[10\% \] là \[x{\rm{ }}(gam,x > 0)\]
Gọi khối lượng dung dịch \[HCl\] \[25\% \] là \[y{\rm{ }}(gam,y > 0)\]
Vì tổng khối lượng hai dung dịch là \[500\] \[gam\] nên ta có phương trình:
\[x + y = 500{\rm{ }}(1)\]
Vì dung dịch tạo thành là \[HCl\] \[16\% \] nên ta có phương trình:
\[10\% x + 25\% y = 16\% .500{\rm{ }}(2)\]
Từ \[(1);{\rm{ }}(2)\] ta có hệ phương trình:
\[\left\{ \begin{array}{l}x + y = 500{\rm{ }}\\10\% x + 25\% y = 16\% .500{\rm{ }}\end{array} \right.\]
\[\left\{ \begin{array}{l}x + y = 500{\rm{ }}\\0,1x + 0,25y = 80{\rm{ }}\end{array} \right.\]
\[\left\{ \begin{array}{l}x + y = 500{\rm{ }}\\x + 2,5y = 800{\rm{ }}\end{array} \right.\]
\[\left\{ \begin{array}{l}x + y = 500{\rm{ }}\\ - 1,5y = - 300{\rm{ }}\end{array} \right.\]
\[\left\{ \begin{array}{l}x = 300{\rm{ }}(tm){\rm{ }}\\y = 200{\rm{ }}(tm){\rm{ }}\end{array} \right.\]
Vậy Bình cần dùng \[300\] \[gam\] dung dịch \[HCl\] \[10\% \] và \[200\]\[gam\] dung dịch \[HCl\] \[25\% \]
Câu hỏi cùng đoạn
Câu 2:
Một nhóm bạn trẻ cùng tham gia khởi nghiệp và dự định góp vốn là \[180\] triệu đồng, số tiền góp mỗi người là như nhau. Nếu có thêm \[3\] người tham gia cùng thì số tiền mỗi người góp giảm đi \[3\] triệu đồng. Hỏi ban đầu nhóm bạn trẻ đó có bao nhiêu người?
Gọi số người ban đầu có là \[x\](người, \[x \in N*\])
Số tiền mỗi người góp lúc đầu là: \[\frac{{180}}{x}\] (triệu đồng)
Số người khi tăng thêm \[3\] người là: \[x + 3\](người)
Số tiền mỗi người góp khi tăng thêm \[3\] người là: \[\frac{{180}}{{x + 3}}\](triệu đồng)
Vì số tiền mỗi người góp giảm đi \[3\] triệu nên ta có phương trình:
\[\frac{{180}}{x} - \frac{{180}}{{x + 3}} = 3\]
\[\frac{{60}}{x} - \frac{{60}}{{x + 3}} = 1\]
\[60\left( {x + 3} \right) - 60x = x(x + 3)\]
\[{x^2} + 3x - 180 = 0\]
\[(x - 12)(x + 15) = 0\]
\[x = 12(TM);x = - 15(KTM)\]
Vậy ban đầu nhóm bạn đó có \[12\] người
Câu 3:
Cho phương trình: \[{x^2} - 2x + m - 1 = 0{\rm{ }}(1)\] với \[m\] là tham số. Tìm tất cả các giá trị của \[m\] để phương trình có hai nghiệm phân biệt thỏa mãn: \[{x_1}{x_2} - 1 = \frac{1}{{{x_1}}} + \frac{1}{{{x_2}}}\]
Cho phương trình: \[{x^2} - 2x + m - 1 = 0{\rm{ }}(1)\] với \[m\] là tham số. Tìm tất cả các giá trị của \[m\] để phương trình có hai nghiệm phân biệt thỏa mãn: \[{x_1}{x_2} - 1 = \frac{1}{{{x_1}}} + \frac{1}{{{x_2}}}\]
Cho phương trình: \[{x^2} - 2x + m - 1 = 0{\rm{ }}(1)\] với \[m\] là tham số.
\[\Delta ' = 1 - m + 1 = 2 - m\]
Phương trình có hai nghiệm phân biệt khi \[\Delta ' > 0 \Leftrightarrow 2 - m > 0 \Leftrightarrow m < 2\]
Áp dụng Định lý Viète ta có:
\[\left\{ \begin{array}{l}{x_1} + {x_2} = 2\\{x_1}.{x_2} = m - 1\end{array} \right.\]
Có: \[{x_1}{x_2} - 1 = \frac{1}{{{x_1}}} + \frac{1}{{{x_2}}}\]
\[{x_1}{x_2} - 1 = \frac{{{x_1} + {x_2}}}{{{x_1}{x_2}}}\]
\[m - 1 - 1 = \frac{2}{{m - 1}}\] (Điều kiện: \[m \ne 1\])
\[(m - 2)(m - 1) = 2\]
\[{m^2} - 3m = 0\]
\[m = 0(TM);m = 3(KTM)\]
Vậy \[m = 0\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
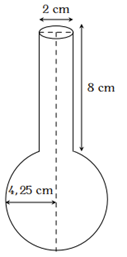
Bán kính đáy phần hình trụ là : \[2:1 = 2(cm)\]
Thể tích của phần bình hình trụ là : \[{V_1} = \pi .{r_1}^2.h = {3,14.1^2}.8 = 25,12(c{m^3})\]
Thể tích phần bình hình cầu là: \[{V_2} = \frac{4}{3}\pi .{r_2}^3 = \frac{4}{3}{.3,14.4,25^3} \approx 321,39(c{m^3})\]
Thể tích nước trong bình là : \[V = 25,12 + 321,39 = 346,51(c{m^3})\]
Vậy thể tích nước trong bình khoảng \[346,51(c{m^3})\]
Lời giải
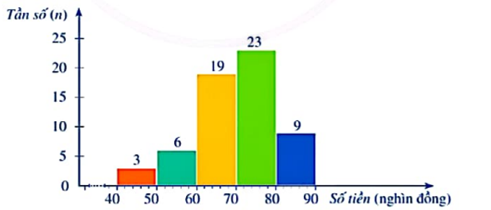
+ Tần số ghép nhóm của nhóm \[\left[ {40;50} \right)\] là \[3\].
+ Tần số tương đối ghép nhóm của nhóm \[\left[ {40;50} \right)\] là: \[\frac{3}{{60}}.100\% = 5\% \]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.