a) Một của hàng kinh doanh xe đạp nhập về một lô hàng gồm hai loại: loại I có giá trị 2 triệu đồng/xe và loại II có giá trị 6 triệu đồng/xe. Biết rằng lô hàng trên có 50 xe với tổng số hàng mà cửa hàng phải thanh toán là 160 triệu đồng. Hỏi cửa hàng đã nhập về bao nhiêu xe loại I và bao nhiêu xe loại II?

b) Bạn An bỏ một viên bi đặc không thấm nước vào một lọ thủy tinh chứa nước dạng hình trụ có bán kính đường tròn đáy bằng 1,5 cm. Biết rằng khi viên bi chìm hoàn toàn trong nước thì nước trong lọ dâng lên thêm 0,5 cm. Tính thể tích viên bi bị bạn An đã bỏ vào lọ thủy tinh (cho \(\pi  \approx 3,14\); xem độ dày của lo không đáng kể và nước trong lọ không thất thoát ra ngoài

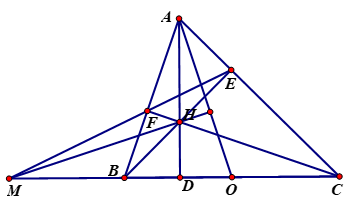
a)  Tứ giác AEHF có:

\(\begin{array}{l}\widehat {{\rm{AEH}}} = {90^0}\left( {BE \bot AC} \right)\\\widehat {{\rm{AFH}}} = {90^0}\left( {CF \bot AB} \right)\end{array}\)

\( \Rightarrow \widehat {{\rm{AEH}}} + \widehat {{\rm{AFH}}} = {180^0}\)

Suy ra tứ giác AEHF nội tiếp ( tổng hai góc đối bằng 1800)

b)    Chứng minh \(\widehat {{\rm{FAD}}} = \widehat {{\rm{OFC}}}\)

Ta có \(\widehat {{\rm{BAD}}} = \widehat {{\rm{FCB}}}\) (cùng phụ với \(\widehat {{\rm{ACB}}}\)) hay \(\widehat {{\rm{FAD}}} = \widehat {{\rm{OCF}}}\) (1)

Mặt khác \(\Delta BFC\) vuông tại F có FO là đường trung tuyến nên FO = OC

Suy ra \(\Delta FCO\)cân tại O suy ra \(\widehat {{\rm{OCF}}} = \widehat {{\rm{OFC}}}\)(2)

Từ (1) và (2) suy ra \(\widehat {{\rm{FAD}}} = \widehat {{\rm{OFC}}}\)

Chứng minh \(O{C^2} = OD \cdot OM\)

Ta dễ dàng chứng minh được các tứ giác AFDC; BFEC nội tiếp

Suy ra \(\widehat {{\rm{BDF}}} = \widehat {{\rm{BAC}}}\)(góc ngoài bằng góc trong tại đỉnh đối)

Lại có \(\widehat {{\rm{ODF}}} = {180^0} - \widehat {{\rm{BDF}}} = {180^0} - \widehat {{\rm{BAC}}}\) (3)

Mặt khác \(\widehat {{\rm{OFM}}} = \widehat {{\rm{OFB}}} + \widehat {{\rm{BFM}}} = \widehat {{\rm{OFB}}} + \widehat {{\rm{AFE}}}\)(\(\widehat {{\rm{BFM}}};\widehat {{\rm{AFE}}}\)đối đỉnh)

Mà \(\left\{ {\begin{array}{*{20}{c}}{\widehat {{\rm{AFE}}} = \widehat {{\rm{ACB}}}}\\{\widehat {{\rm{ACB}}} = \widehat {{\rm{OFB}}}}\end{array}} \right.\)   Suy ra \(\widehat {{\rm{OFM}}} = \widehat {{\rm{ABC}}} + \widehat {{\rm{ACB}}} = {180^0} - \widehat {{\rm{BAC}}}\)(4)

Từ (3) và (4) suy ra \(\widehat {{\rm{ODF}}} = \widehat {{\rm{OFM}}}\)

Xét \(\Delta OFD\)và \(\Delta OMF\)có:\(\widehat {{\rm{ODF}}} = \widehat {{\rm{OFM}}}\)(cmt);  \(\widehat {MOF}\)chung

Suy ra \(\Delta OFD\)\( \sim \Delta OMF\)(gg)

Suy ra \[\frac{{FO}}{{OM}} = \frac{{OD}}{{FO}}{\rm{O}}{{\rm{F}}^2} = OM \cdot OD = O{C^2}\](vì O là trung điểm BC)

c)

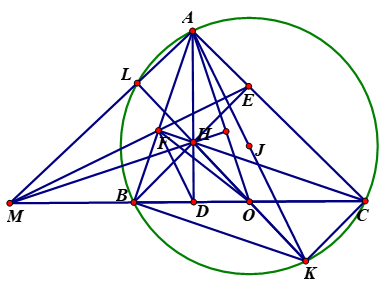
Gọi AK là đường kính của đường tròn ngoại tiếp tam giác ABC

Suy ra AB vuông góc với BK mà CH vuông góc với AB nên CH song song với BK

Chứng minh tương tự BH song song với CK

Do đó tứ giác BHCK là hình bình hành nên ba điểm O. H, K thẳng hàng (1).

Gọi L là giao điểm của AM với đường tròn ngoại tiếp tam giác ABC

Do các tứ giác ALBC và BFEC nội tiếp nên ta có

ML.MA=MB.MC=MF.ME

Suy ra tứ giac ALFE nội tiếp nên suy ra \(\widehat {{\rm{ALH}}} = \widehat {{\rm{AFH}}} = {90^0}\) (cùng chắn cung AH)

Suy ra AL vuông góc với HL.

Mà AL vuông góc với LK (góc nội tiếp chắn nữa đường tròn)

Nên bốn điểm L, H, O, K thảng hàng do đó OL vuông góc với AM

Vậy H là trực tâm của tam giác AMO  suy ra MH vuông góc với AO

a) Giải phương trình \({x^2} + 3x - 10 = 0\)

\(\begin{array}{l}\Delta  = {b^2} - 4ac\\\Delta  = {3^2} - 4 \cdot 1 \cdot \left( { - 10} \right) = 49 > 0\end{array}\)

Nên phương trình có hai nghiệm phân biệt \({x_1} = \frac{{ - b - \sqrt \Delta  }}{{2a}} = \frac{{ - 3 - \sqrt {49} }}{2} =  - 5\); \({x_1} = \frac{{ - b + \sqrt \Delta  }}{{2a}} = \frac{{ - 3 + \sqrt {49} }}{2} = 2\)

Vậy tập nghiệm của phương trình là \(S = \left\{ { - 5;2} \right\}\)

b)    Phương trình \({x^2} - 5x + 3 = 0\) có \(\Delta  = {\left( { - 5} \right)^2} - 4 \cdot 3 = 13 > 0\)nên phương trình có hai nghiệm phân biệt x1, x2.

Theo định lý Viets ta có \(\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} = 5}\\{{x_1} \cdot {x_2} = 3}\end{array}} \right.\)

Vì \({x_1} + {x_2} = 5 > 0;\,\,\,{x_1} \cdot {x_2} = 3 > 0\) nên phương trình có hai nghiệm dương và do x1 là nghiệm của phương trình (1) nên \({x_1}^2 - 5{x_1} + 3 = 0\, \Rightarrow {x_1}^2 = 5{x_1} - 3\)

Do đó

\(\begin{array}{l}T = \frac{{\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)}}{{{x_1}^2 + 5{x_2}}}\\T = \frac{{{x_1} \cdot {x_2} + {x_1} + {x_2} + 1}}{{5\left( {{x_1} + {x_2}} \right) - 3}} = \frac{{3 + 5 + 1}}{{5 \cdot 5 - 3}} = \frac{9}{{22}}\end{array}\)