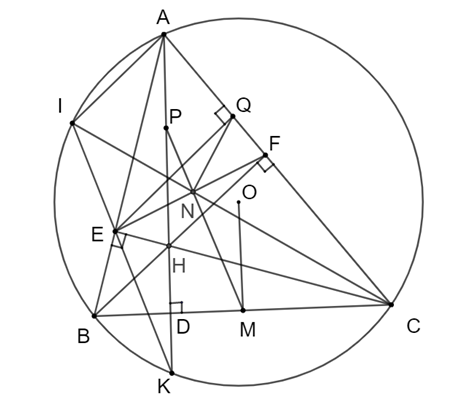
Cho \(\Delta ABC\)có ba góc nhọn nội tiếp đường tròn \(\left( {O;R} \right)\). Các đường cao \(AD,\,BF,CE\)của \(\Delta ABC\) cắt nhau tại \(H\).

a) Chứng minh tứ giác \(BEHD\) nội tiếp một đường tròn.

b) Kéo dài \(AD\)cắt đường tròn \(\left( O \right)\)tại điểm thứ hai \(K\). Kéo dài \(KE\)cắt đường tròn \(\left( O \right)\)tại điểm thứ hai \(I\). Gọi \(N\)là giao điểm của \(CI\)và \(EF\). Chứng minh \(C{E^2} = CN.CI\).

c) Kẻ \(OM\) vuông góc với \(BC\) tại \(M\). Gọi \(P\) là tâm đường tròn ngoại tiếp \(\Delta AEF\). Chứng minh ba điểm \(M,\,N,\,P\) thẳng hàng.

a)Chỉ ra được \(\widehat {BEH} = {90^{\rm{o}}}\)

Chỉ ra được \(\widehat {BDH} = {90^{\rm{o}}}\)

Suy ra tứ giác \(BEHD\) có \(\widehat {BEH}\, + \widehat {BDH}\, = {180^{\rm{o}}}\) và  \(\widehat {BEH}\), \(\widehat {BDH}\) là hai góc ở vị trí đối diện nhau

Kết luận tứ giác \(BEHD\) nội tiếp được trong một đường tròn.

 b)Ta có \(\widehat {CIK} = \widehat {CAK}\) (cùng bằng )

Chỉ ra tứ giác \(AEHF\) nội tiếp (Tổng hai góc đối bằng \(180^\circ \)) \( \Rightarrow \widehat {FAH} = \widehat {FEH}\).

Suy ra \(\widehat {CIE} = \widehat {NEC}\)

Chỉ ra hai tam giác \(CIE\) và \(CEN\) đồng dạng theo trường hợp góc – góc

\( \Rightarrow \frac{{CE}}{{CN}} = \frac{{CI}}{{CE}} \Rightarrow C{E^2} = CN.CI\) (đpcm)

Chỉ ra \(P\) là tâm đường tròn ngoại tiếp tam giác \(AEF\) cũng là tâm đường tròn ngoại tiếp tứ giác \(AEHF\).

Chỉ ra \(M\) là tâm đường tròn ngoại tiếp tứ giác \(BEFC\).

Mà hai tứ giác \(AEHF\)và \(BEFC\)có hai điểm chung là \(EF\)nên \(PM\)đi qua trung điểm của \(EF\,\left( 1 \right)\)

Gọi \(Q\) là hình chiếu của \(E\) trên \(AC\). Xét \(\Delta EAC\)vuông tại \(E\), có \(EQ\) là đường cao nên \(C{E^2} = CQ.CA\)

Theo b) ta có \(C{E^2} = CN.CI\) nên \(CN.CI = CQ.CA \Rightarrow \frac{{CN}}{{CQ}} = \frac{{CA}}{{CI}}\)

Suy ra hai tam giác \(CNQ;\,CAI\) đồng dạng (chung góc \(C\) và tỉ số bằng nhau)

\( \Rightarrow \widehat {CQN} = \widehat {CIA}\). Mà \(\widehat {CIA} = \widehat {CBA}\) (góc nội tiếp cùng chắn cung ) \( \Rightarrow \widehat {CQN} = \widehat {CBA}\)

Do tứ giác \(BEFC\)nội tiếp nên \(\widehat {QFN} = \widehat {EBC}\) (Cùng bù với góc \(\widehat {CFE}\))

Suy ra \(\widehat {CQN} = \widehat {FQN} = \widehat {QFN} \Rightarrow NQ = NF\)

Chỉ ra \(\widehat {NQE} = \widehat {QEN}\) (Tương ứng phụ với hai góc bằng nhau \(\widehat {FQN};\,\widehat {QFN}\)) \( \Rightarrow NQ = NE\)

Do đó \(NE = NF\)hay \(N\) là trung điểm của \(EF\,\left( 2 \right)\)