Cho đường tròn tâm \(O\) đường kính \(BC\). Trên đường tròn đã cho lấy điểm \(A\) cố định (\(A\) khác \(B\) và \(C\)) và lấy điểm \(D\) thay đổi trên cung nhỏ \(AC\) (\(D\) khác \(A\) và \(C\)). Kẻ \(AH\) vuông góc với \(BC\) (\(H\) thuộc \(BC\)). Hai đường thẳng \(BD\) và \(AH\) cắt nhau tại \(I\).

1) Chứng minh rằng tứ giác \(IHCD\) là tứ giác nội tiếp.

2) Chứng minh rằng \(A{B^2} = BI \cdot BD\).

3) Lấy điểm \(M\) trên đoạn thẳng \(BC\) sao cho \(BM = AB\). Chứng minh rằng tâm đường tròn ngoại tiếp \(\Delta MID\) luôn nằm trên một đường thẳng cố định khi \(D\) thay đổi trên cung nhỏ \(AC\).

a)Học sinh vẽ đúng hình để làm được ý a)

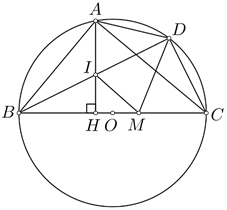
Vì \(AH \bot BC\) nên \(\widehat {IHC} = 90^\circ \)

\(\widehat {BDC}\) là góc nội tiếp chắn nửa đường tròn nên \(\widehat {BDC} = 90^\circ \)

Ta có: \(\widehat {IHC} + \widehat {BDC} = 90^\circ  + 90^\circ  = 180^\circ \)

Vậy tứ giác \(IHCD\) nội tiếp.

b)Ta có:  \(\left( 1 \right)\)

\(\Delta ABH\) vuông tại \(H\) \( \Rightarrow \widehat {BAI} + \widehat {ABC} = 90^\circ \) \(\left( 2 \right)\)

\(\widehat {BAC} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \widehat {ACB} + \widehat {ABC} = 90^\circ \) \(\left( 3 \right)\)

Từ \(\left( 1 \right)\); \(\left( 2 \right)\) và \(\left( 3 \right)\) \( \Rightarrow \widehat {BAI} = \widehat {ADB}\)

Xét \(\Delta BAI\) và \(\Delta BDA\) có: \(\widehat {ABD}\) chung; \(\widehat {BAI} = \widehat {ADB}\)

 (g-g) \( \Rightarrow \frac{{AB}}{{BD}} = \frac{{BI}}{{AB}}\)\( \Rightarrow A{B^2} = BI \cdot BD\)

c)Do \(BM = AB\), mà \(\frac{{AB}}{{BD}} = \frac{{BI}}{{AB}}\) nên \(B{M^2} = BI \cdot BD\)\( \Rightarrow \frac{{BM}}{{BD}} = \frac{{BI}}{{BM}}\)

Xét \(\Delta BMI\) và \(\Delta BDM\) có: \(\widehat {DBM}\) chung; \(\frac{{BM}}{{BD}} = \frac{{BI}}{{BM}}\)

 (c-g-c) \( \Rightarrow \widehat {BMI} = \widehat {BDM}\)

\( \Rightarrow BM\) là tiếp tuyến tại \(M\) của đường tròn ngoại tiếp \(\Delta MID\)

Suy ra tâm đường tròn ngoại tiếp \(\Delta MID\) thuộc đường thẳng vuông góc với \(BC\) tại \(M\)

Do \(A\); \(B\); \(C\) cố định nên \(M\) cố định và đường thẳng vuông góc với \(BC\) tại \(M\) cố định

Vậy tâm đường tròn ngoại tiếp \(\Delta MID\) luôn nằm trên một đường thẳng cố định khi \(D\) thay đổi trên cung nhỏ \(AC\).