Cho tam giác \(ABC\) nội tiếp đường tròn tâm \(O\). Kẻ \(AH\) vuông góc với \(BC\) tại \(H\), kẻ \(HE\) vuông góc với \(AB\) tại \(E\), kẻ \(HD\) vuông góc với \(AC\) tại \(D\).
a) Chứng minh: tứ giác \(AEHD\) là tứ giác nội tiếp.
b) Dựng đường kính \(AK\) của đường tròn \(\left( O \right)\). Chứng minh \(AE.AK = AH.AC\)
Cho tam giác \(ABC\) nội tiếp đường tròn tâm \(O\). Kẻ \(AH\) vuông góc với \(BC\) tại \(H\), kẻ \(HE\) vuông góc với \(AB\) tại \(E\), kẻ \(HD\) vuông góc với \(AC\) tại \(D\).
a) Chứng minh: tứ giác \(AEHD\) là tứ giác nội tiếp.
b) Dựng đường kính \(AK\) của đường tròn \(\left( O \right)\). Chứng minh \(AE.AK = AH.AC\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
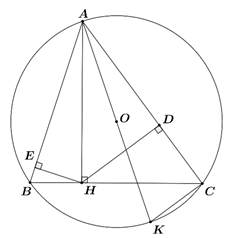
a) Tứ giác \(AEHD\) có:
\(\begin{array}{l}\widehat {AEH} = 90^\circ \,\,\,\,\left( {HE \bot AB} \right)\\\widehat {ADH} = 90^\circ \,\,\,\,\left( {HD \bot AC} \right)\end{array}\)
\( \Rightarrow \widehat {AEH} + \widehat {ADH} = 180^\circ \)
Vậy tứ giác \(AEHD\) nội tiếp
b) Ta có \(\widehat {ACK} = 90^\circ \)(góc nội tiếp chắn nửa đường tròn)
\(\begin{array}{l}\widehat {EAH} + \widehat {ABH} = 90^\circ \\\widehat {CAK} + \widehat {AKC} = 90^\circ \end{array}\)
mà \[\widehat {ABH} = \widehat {AKC}\] (cùng chắn cung \(AC\))
\( \Rightarrow \widehat {EAH} = \widehat {CAK}\)
Xét \(\Delta EAH\) và \(\Delta CAK\) có:
\(\widehat {EAH} = \widehat {ACK} = 90^\circ \)
\(\widehat {EAH} = \widehat {CAK}\) (cmt)
\(\begin{array}{l} \Rightarrow \frac{{AE}}{{AC}} = \frac{{AH}}{{AK}}\\ \Rightarrow AE.AK = AH.AC\end{array}\)
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(x\) là số bài tập mỗi ngày bạn A phải làm theo kế hoạch ban đầu
Điều kiện: \(x \in \mathbb{N},\,0 < x < 80\)
Trên thực tế mỗi ngày bạn A phải làm là \(x + 2\) bài tập
Theo kế hoạch số ngày để bạn A hoàn thành 80 bài tập là \(\frac{{80}}{x}\) (ngày)
Do bạn A hoàn thành sớm hơn 2 ngày so với kế hoạch ban đầu nên ta có phương trình:
\(\frac{{80}}{x} - \frac{{80}}{{x + 2}} = 2\)
Giải phương trình ta được \(x = 8\) (thỏa điều kiện)
Vậy theo kế hoạch mỗi ngày bạn A phải làm xong 8 bài tập.
Câu 2
Lời giải
Chọn D
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập