Cho hai số thực dương \(a\) và \(b\) thỏa mãn \(a + b \le 2\). Chứng minh \(\frac{{{a^2}}}{{{a^2} + b}} + \frac{{{b^2}}}{{{b^2} + a}} \le 1\).

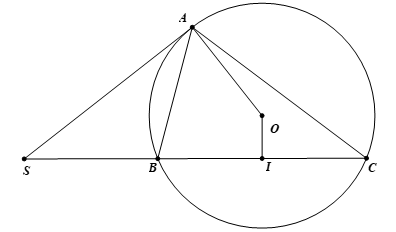
1) Chứng minh tứ giác \(SAOI\) là tứ giác nội tiếp.

Tứ giác \(SAOI\) có: \(\widehat {SAO} = 90^\circ \) (tính chất của tiếp tuyến); \(\widehat {SIO} = 90^\circ \) (\(OI \bot BC\));

\(\widehat {SAO} + \widehat {SIO} = 90^\circ  + 90^\circ  = 180^\circ \)

Hai góc \(\widehat {SAO}\) và \(\widehat {SIO}\) đối nhau

\( \Rightarrow \) Tứ giác \(SAOI\) nội tiếp đường tròn đường kính \(SO\).

2) Gọi \(H\) và \(D\) lần lượt là chân các đường vuông góc kẻ từ điểm \[{\rm{A}}\] đến các đường thẳng \(SO\) và \(SC\). Chứng minh \(\widehat {OAH} = \widehat {IAD}\).

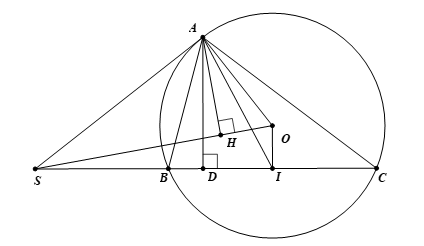
Theo ý a), ta có: Tứ giác \(SAOI\) nội tiếp nên \(\widehat {SOA} = \widehat {SIA}\) (hai góc nội tiếp cùng chắn );

\( \Rightarrow 90^\circ  - \widehat {SOA} = 90^\circ  - \widehat {SIA}\);

Mà \(90^\circ  - \widehat {SOA} = \widehat {OAH}\) (\(\Delta AHO\) vuông tại \(H\)); \(90^\circ  - \widehat {SIA} = \widehat {IAD}\) (\[\Delta ADI\] vuông tại \(D\))

\( \Rightarrow \widehat {OAH} = \widehat {IAD}\).

3) Vẽ đường cao \(CE\) của tam giác \(ABC\). Gọi \(Q\) là trung điểm của đoạn thẳng \(BE\). Đường thẳng \(QD\) cắt đường thẳng \(AH\) tại điểm \(K\). Chứng minh \(BQ.BA = BD.BI\) và đường thẳng \(CK\) song song với đường thẳng \(SO\).

Vì \(OI \bot BC \Rightarrow I\) là trung điểm của \(BC\) (quan hệ vuông góc giữa đường kính và dây), mà \(Q\) là ttrung điểm của \(BE \Rightarrow IQ\) là đường trung bình của \(\Delta BEC \Rightarrow IQ{\rm{//}}CE\) mà \(CE \bot AB \Rightarrow IQ \bot AB \Rightarrow \widehat {IQA} = 90^\circ \), lại có \(\widehat {IDA} = 90^\circ \left( {AD \bot SC} \right) \Rightarrow \) Tứ giác \(AQDI\) nội tiếp đường tròn đường kính \(AI \Rightarrow \) \(\widehat {QAI} + \widehat {QDI} = 180^\circ \) mà \(\widehat {BDQ} + \widehat {QDI} = 180^\circ \) (hai góc kề bù) \( \Rightarrow \widehat {BDQ} = \widehat {QAI}\left( { = 180^\circ  - \widehat {QDI}} \right)\).

Xét \(\Delta BDQ\) và \(\Delta BAI\) có:

\(\widehat B\) chung; \(\widehat {BDQ} = \widehat {BAI}\) (chứng minh trên);

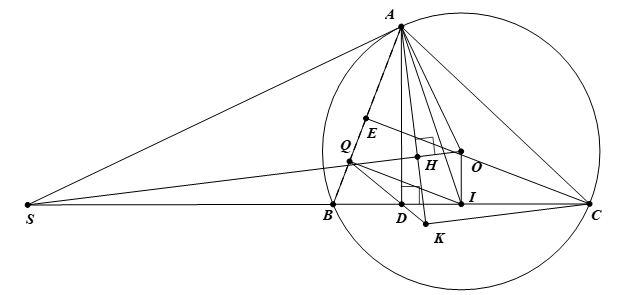
\( \Rightarrow \frac{{BD}}{{BQ}} = \frac{{BA}}{{BI}} \Rightarrow BQ.BA = BD.BI\).

Vì \(\widehat {BDQ} = \widehat {KDC}\) (hai góc đối đỉnh) \( \Rightarrow \widehat {KDC} = \widehat {BAI}\) (1);

Ta có: \(\widehat {SAB} + \widehat {BAO} = 90^\circ \left( {SA \bot OA} \right)\); \(\widehat {DAC} + \widehat {ACD} = 90^\circ \) (\(\Delta ADC\) vuông tại \(D\)); mà \(\widehat {BCA} = \widehat {SAB}\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn )

\( \Rightarrow \widehat {BAO} = \widehat {DAC}\) hay \(\widehat {BAD} = \widehat {OAC}\) lại có \(\widehat {DAI} = \widehat {HAO}\) (ý 2)) \( \Rightarrow \widehat {BAI} = \widehat {KAC}\) (2);

Từ (1) và (2), ta có: \(\widehat {KAC} = \widehat {KDC} \Rightarrow \) tứ giác \(DKCA\) nội tiếp

\( \Rightarrow \widehat {ADC} = \widehat {AKC} = 90^\circ  \Rightarrow AK \bot CK\), mà \(AK \bot SO \Rightarrow SO{\rm{//}}KC\).

1) Gọi số sản phẩm mỗi ngày phân xưởng phải làm theo kế hoạch là \(x\) (sản phẩm), \(x \in \mathbb{N}*,\,\,x < 900\).

Thời gian phân xưởng phải hoàn thành theo kế hoạch là \(\frac{{900}}{x}\) (ngày)

Thực tế, mỗi ngày phân xưởng làm được \(x + 15\) (sản phẩm)

Thời gian phân xưởng hoàn thành trên thực tế là \(\frac{{900}}{{x + 15}}\) (ngày)

Vì phân xưởng hoàn thành trước thời hạn 3 ngày nên ta có phương trình:

\(\frac{{900}}{x} - \frac{{900}}{{x + 15}} = 3\)

\( \Rightarrow 900(x + 15) - 900x = 3x(x + 15)\)

\(\begin{array}{l} \Leftrightarrow 3{x^2} + 45x - 13500 = 0\\ \Leftrightarrow {x^2} + 15x - 4500 = 0\end{array}\)

Tìm được \(x = 60\) (thoả mãn), \(x =  - 75\) (loại)

Vậy theo kế hoạch, mỗi ngày phân xưởng phải làm \(60\)sản phẩm.

2) Một khối gỗ dạng hình trụ có bán kính đáy là \(30{\rm{\;cm}}\) và chiều cao là \(120{\rm{\;cm}}\). Tính thể tích của khối gỗ đó. (lấy \(\pi  \approx 3,14)\).

Thể tích khối gỗ: \(V = \pi {r^2}h \approx 3,{14.30^2}.120 = 339120\,\left( {c{m^3}} \right)\)

Vậy thể tích khối gỗ khoảng \(339120\,\left( {c{m^3}} \right)\)