\[\begin{array}{l} = \frac{{\left( {2\sqrt x - 3} \right)\left( {\sqrt x + 1} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} + \frac{{3 - \sqrt x }}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\\ = \frac{{2x + 2\sqrt x - 3\sqrt x - 3 + 3 - \sqrt x }}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\\ = \frac{{2x - 2\sqrt x }}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} = \frac{{2\sqrt x \left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\\ = \frac{{2\sqrt x }}{{\sqrt x + 1}}\end{array}\]

Vậy $B = \frac{{2\sqrt x }}{{\sqrt x + 1}}$ ( đpcm)

c) với $x > 0,x \ne 1.$ta có: $A.B = \frac{{x + 2}}{{\sqrt x }}.\frac{{2\sqrt x }}{{\sqrt x + 1}} = \frac{{2x + 4}}{{\sqrt x + 1}}$

đề $A.B = 4 \Leftrightarrow \frac{{2x + 4}}{{\sqrt x + 1}} = 4$ $ \Leftrightarrow \frac{{2x + 4}}{{\sqrt x + 1}} = \frac{{4\left( {\sqrt x + 1} \right)}}{{\sqrt x + 1}}$

$\begin{array}{l} \Rightarrow 2x + 4 = 4\sqrt x + 4 \Leftrightarrow 2x - 4\sqrt x = 0\\ \Leftrightarrow 2\sqrt x \left( {\sqrt x - 2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}2\sqrt x = 0\\\sqrt x - 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 4\end{array} \right.\end{array}$

Đối chiếu với điều kiện ta được $x = 4$ là giá trị cần tìm.

Câu 2

1) Giải bài toán sau bằng cách lập phương trình hoăc hệ phuơng trình:

Theo kế hoạch, một phân xưởng phải làm xong 900 sản phẩm trong một số ngày quy định. Thực tế, mỗi ngày phân xưởng đã làm được nhiều hơn 15 sản phẩm so với số sản phẩm phải làm trong một ngày theo kế hoạch. Vì thế 3 ngày trước khi hết thời hạn, phân xưởng đã làm xong 900 sản phẩm. Hỏi theo kế hoạch, mỗi ngày phân xưởng phải làm bao nhiêu sản phẩm? (Giả định rằng số sản phẩm mà phân xưởng làm được trong mỗi ngày là bằng nhau.)

2) Một khối gỗ dạng hình trụ có bán kính đáy là $30{\rm{\;cm}}$ và chiều cao là $120{\rm{\;cm}}$. Tính thể tích của khối gỗ đó. (lấy $\pi \approx 3,14)$.

Xem đáp án

Lời giải

1) Gọi số sản phẩm mỗi ngày phân xưởng phải làm theo kế hoạch là $x$ (sản phẩm), $x \in \mathbb{N}*,\,\,x < 900$.

Thời gian phân xưởng phải hoàn thành theo kế hoạch là $\frac{{900}}{x}$ (ngày)

Thực tế, mỗi ngày phân xưởng làm được $x + 15$ (sản phẩm)

Thời gian phân xưởng hoàn thành trên thực tế là $\frac{{900}}{{x + 15}}$ (ngày)

Vì phân xưởng hoàn thành trước thời hạn 3 ngày nên ta có phương trình:

$\frac{{900}}{x} - \frac{{900}}{{x + 15}} = 3$

$ \Rightarrow 900(x + 15) - 900x = 3x(x + 15)$

$\begin{array}{l} \Leftrightarrow 3{x^2} + 45x - 13500 = 0\\ \Leftrightarrow {x^2} + 15x - 4500 = 0\end{array}$

Tìm được $x = 60$ (thoả mãn), $x = - 75$ (loại)

Vậy theo kế hoạch, mỗi ngày phân xưởng phải làm $60$sản phẩm.

2) Một khối gỗ dạng hình trụ có bán kính đáy là $30{\rm{\;cm}}$ và chiều cao là $120{\rm{\;cm}}$. Tính thể tích của khối gỗ đó. (lấy $\pi \approx 3,14)$.

Thể tích khối gỗ: $V = \pi {r^2}h \approx 3,{14.30^2}.120 = 339120\,\left( {c{m^3}} \right)$

Vậy thể tích khối gỗ khoảng $339120\,\left( {c{m^3}} \right)$

Câu 3

1) Giải hệ phương trình $\left\{ {\begin{array}{*{20}{l}}{\frac{2}{{x - 3}} - 3y = 1}\\{\frac{3}{{x - 3}} + 2y = 8}\end{array}} \right.$.

2) Trong mặt phẳng tọa độ Oxy, cho parabol $y = {x^2}$ và đường thẳng (d): $y = (m + 2)x - m.$

Xem đáp án

Lời giải

1). $\left\{ {\begin{array}{*{20}{l}}{\frac{2}{{x - 3}} - 3y = 1}\\{\frac{3}{{x - 3}} + 2y = 8}\end{array}} \right.$ điều kiện: $x \ne 3$.

Đặt $\frac{1}{{x - 3}} = a$ hệ phương trình trở thành: $\left\{ {\begin{array}{*{20}{l}}{2a - 3y = 1}\\{3a + 2y = 8}\end{array}} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\y = 1\end{array} \right.$.

Với $a = 2 \Rightarrow \frac{1}{{x - 3}} = 2 \Rightarrow x = \frac{7}{2}$.

Vậy hệ phương trình có nghiệm $\left( {x;\,y} \right) = \left( {\frac{7}{2};\,1} \right)$.

Xét phương trình hoành độ giao điểm $\left( d \right)$ và $\left( P \right)$.

${x^2} = (m + 2)x - m$

$ \Leftrightarrow {x^2} - (m + 2)x + m = 0$(*)

Ta có $\Delta = {(m + 2)^2} - 4.1.m \Rightarrow \Delta = {m^2} + 4$.

Do ${m^2} \ge 0$ với mọi $m \Rightarrow {m^2} + 4 > 0$ với mọi $m$

$ \Rightarrow \Delta > 0$ với mọi $m$, Phương trình (*) luôn có hai nghiệm phân biệt với mọi $m$.

Vậy $\left( d \right)$ luôn cắt $\left( P \right)$ tại hai điểm phân biệt với mọi $m$.

b) Gọi ${x_1}$ và ${x_2}$ là hoành độ các giao điểm của $\left( d \right)$ và $\left( P \right)$. Tìm tất cả giá trị của $m$ để

$\frac{1}{{{x_1}}} + \frac{1}{{{x_2}}} = \frac{1}{{{x_1} + {x_2} - 2}}$

Theo hệ thức Vi - et ta có: \[\left\{ \begin{array}{l}{x_1} + {x_2} = m + 2\\{x_1}{x_2} = m\end{array} \right.\]

Điều kiện để biểu thức $\frac{1}{{{x_1}}} + \frac{1}{{{x_2}}} = \frac{1}{{{x_1} + {x_2} - 2}}$có nghĩa: \[\left\{ \begin{array}{l}{x_1} \ne 0\\{x_2} \ne 0\\{x_1} + {x_2} \ne 2\end{array} \right.\]

Khi đó: \[\left\{ \begin{array}{l}m + 2 \ne 2\\m \ne 0\end{array} \right. \Leftrightarrow m \ne 0\]

Xét: $\frac{1}{{{x_1}}} + \frac{1}{{{x_2}}} = \frac{1}{{{x_1} + {x_2} - 2}}$

$ \Leftrightarrow \frac{{{x_1} + {x_2}}}{{{x_1}.{x_2}}} = \frac{1}{{{x_1} + {x_2} - 2}}$

$ \Leftrightarrow \frac{{m + 2}}{m} = \frac{1}{{m + 2 - 2}}$

$ \Leftrightarrow \frac{{m + 2}}{m} = \frac{1}{m}$

$ \Leftrightarrow m + 2 = 1$

$ \Leftrightarrow m = - 1$(Thỏa mãn điều kiện)

Vậy với $m = - 1$thì thỏa mãn yêu cầu bài toán

Câu 4

Cho tam giác $ABC$ có ba góc nhọn ($AB < AC$), nội tiếp đường tròn $\left( O \right)$. Tiếp tuyến

tại điểm $A$ của đường tròn $\left( O \right)$ cắt đường thẳng $BC$ tại điểm $S$. Gọi $I$ là chân đường vuông góc

kẻ từ điểm $O$ đến đường thẳng $BC$.

1) Chứng minh tứ giác $SAOI$ là tứ giác nội tiếp.

2) Gọi $H$ và $D$ lần lượt là chân các đường vuông góc kẻ từ điểm \[{\rm{A}}\] đến các đường thẳng $SO$ và

$SC$. Chứng minh $\widehat {OAH} = \widehat {IAD}$.

3) Vẽ đường cao $CE$ của tam giác $ABC$. Gọi $Q$ là trung điểm của đoạn thẳng $BE$. Đường thẳng

$QD$ cắt đường thẳng $AH$ tại điểm $K$. Chứng minh $BQ.BA = BD.BI$ và đường thẳng $CK$ song

song với đường thẳng $SO$.

Xem đáp án

Lời giải

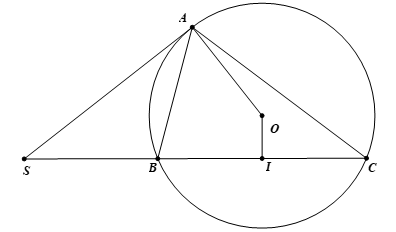
$Cho tam giác $ABC$ có ba góc nhọn ($AB < AC$), nội tiếp đường tròn $\left( O \right)$. Tiếp tuyến (ảnh 1)$

1) Chứng minh tứ giác $SAOI$ là tứ giác nội tiếp.

Tứ giác $SAOI$ có: $\widehat {SAO} = 90^\circ $ (tính chất của tiếp tuyến); $\widehat {SIO} = 90^\circ $ ($OI \bot BC$);

$\widehat {SAO} + \widehat {SIO} = 90^\circ + 90^\circ = 180^\circ $

Hai góc $\widehat {SAO}$ và $\widehat {SIO}$ đối nhau

$ \Rightarrow $ Tứ giác $SAOI$ nội tiếp đường tròn đường kính $SO$.

2) Gọi $H$ và $D$ lần lượt là chân các đường vuông góc kẻ từ điểm \[{\rm{A}}\] đến các đường thẳng $SO$ và $SC$. Chứng minh $\widehat {OAH} = \widehat {IAD}$.

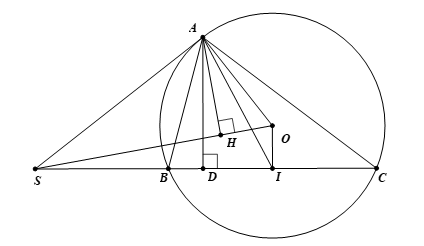
$Cho tam giác $ABC$ có ba góc nhọn ($AB < AC$), nội tiếp đường tròn $\left( O \right)$. Tiếp tuyến (ảnh 2)$

Theo ý a), ta có: Tứ giác $SAOI$ nội tiếp nên $\widehat {SOA} = \widehat {SIA}$ (hai góc nội tiếp cùng chắn );

$ \Rightarrow 90^\circ - \widehat {SOA} = 90^\circ - \widehat {SIA}$;

Mà $90^\circ - \widehat {SOA} = \widehat {OAH}$ ($\Delta AHO$ vuông tại $H$); $90^\circ - \widehat {SIA} = \widehat {IAD}$ (\[\Delta ADI\] vuông tại $D$)

$ \Rightarrow \widehat {OAH} = \widehat {IAD}$.

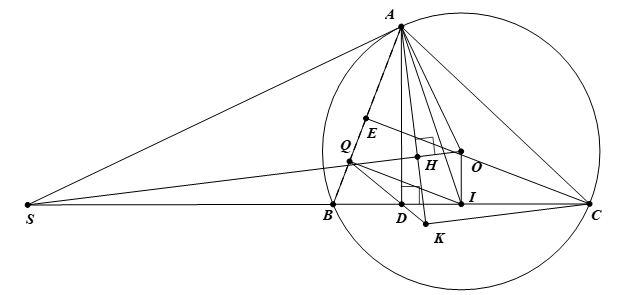
3) Vẽ đường cao $CE$ của tam giác $ABC$. Gọi $Q$ là trung điểm của đoạn thẳng $BE$. Đường thẳng $QD$ cắt đường thẳng $AH$ tại điểm $K$. Chứng minh $BQ.BA = BD.BI$ và đường thẳng $CK$ song song với đường thẳng $SO$.

Vì $OI \bot BC \Rightarrow I$ là trung điểm của $BC$ (quan hệ vuông góc giữa đường kính và dây), mà $Q$ là ttrung điểm của $BE \Rightarrow IQ$ là đường trung bình của $\Delta BEC \Rightarrow IQ{\rm{//}}CE$ mà $CE \bot AB \Rightarrow IQ \bot AB \Rightarrow \widehat {IQA} = 90^\circ $, lại có $\widehat {IDA} = 90^\circ \left( {AD \bot SC} \right) \Rightarrow $ Tứ giác $AQDI$ nội tiếp đường tròn đường kính $AI \Rightarrow $ $\widehat {QAI} + \widehat {QDI} = 180^\circ $ mà $\widehat {BDQ} + \widehat {QDI} = 180^\circ $ (hai góc kề bù) $ \Rightarrow \widehat {BDQ} = \widehat {QAI}\left( { = 180^\circ - \widehat {QDI}} \right)$.

Xét $\Delta BDQ$ và $\Delta BAI$ có:

$\widehat B$ chung; $\widehat {BDQ} = \widehat {BAI}$ (chứng minh trên);

$Cho tam giác $ABC$ có ba góc nhọn ($AB < AC$), nội tiếp đường tròn $\left( O \right)$. Tiếp tuyến (ảnh 3)$

$ \Rightarrow \frac{{BD}}{{BQ}} = \frac{{BA}}{{BI}} \Rightarrow BQ.BA = BD.BI$.

Vì $\widehat {BDQ} = \widehat {KDC}$ (hai góc đối đỉnh) $ \Rightarrow \widehat {KDC} = \widehat {BAI}$ (1);

Ta có: $\widehat {SAB} + \widehat {BAO} = 90^\circ \left( {SA \bot OA} \right)$; $\widehat {DAC} + \widehat {ACD} = 90^\circ $ ($\Delta ADC$ vuông tại $D$); mà $\widehat {BCA} = \widehat {SAB}$ (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn )

$ \Rightarrow \widehat {BAO} = \widehat {DAC}$ hay $\widehat {BAD} = \widehat {OAC}$ lại có $\widehat {DAI} = \widehat {HAO}$ (ý 2)) $ \Rightarrow \widehat {BAI} = \widehat {KAC}$ (2);

Từ (1) và (2), ta có: $\widehat {KAC} = \widehat {KDC} \Rightarrow $ tứ giác $DKCA$ nội tiếp

$ \Rightarrow \widehat {ADC} = \widehat {AKC} = 90^\circ \Rightarrow AK \bot CK$, mà $AK \bot SO \Rightarrow SO{\rm{//}}KC$.

Câu 5

Cho hai số thực dương $a$ và $b$ thỏa mãn $a + b \le 2$. Chứng minh $\frac{{{a^2}}}{{{a^2} + b}} + \frac{{{b^2}}}{{{b^2} + a}} \le 1$.

Xem đáp án

Lời giải

Cách 1: Ta có $\frac{{{a^2}}}{{{a^2} + b}} + \frac{{{b^2}}}{{{b^2} + a}} \le 1$

$ \Leftrightarrow {a^2}\left( {{b^2} + a} \right) + {b^2}\left( {{a^2} + b} \right) \le \left( {{a^2} + b} \right)\left( {{b^2} + a} \right)$ hay${a^2}{b^2} \le ab$

Sử dụng bất đẳng thức Cô si, ta có $2 \ge a + b \ge 2\sqrt {ab} $. Suy ra $ab \le 1$.

Từ đó ${a^2}{b^2} \le ab$. Ta có điều phải chứng minh.

Dấu đẳng thức xảy ra khi và chỉ khi $a = b = 1$.

Cách 2: Có $P = \frac{{{a^2}}}{{{a^2} + b}} + \frac{{{b^2}}}{{{b^2} + a}} = \frac{{{a^2} + b - b}}{{{a^2} + b}} + \frac{{{b^2} + a - a}}{{{b^2} + a}} = 2 - \left( {\frac{b}{{{a^2} + b}} + \frac{a}{{{b^2} + a}}} \right)$

Ta có: $\frac{b}{{{a^2} + b}} + \frac{a}{{{b^2} + a}} = \frac{{{b^2}}}{{{a^2}b + {b^2}}} + \frac{{{a^2}}}{{{b^2}a + {a^2}}}$$ \ge \frac{{{{\left( {a + b} \right)}^2}}}{{{a^2} + {b^2} + ab\left( {a + b} \right)}}$

Mà $a + b \le 2 \Rightarrow {a^2} + {b^2} + ab\left( {a + b} \right) \le {\left( {a + b} \right)^2}$

$ \Rightarrow \frac{b}{{{a^2} + b}} + \frac{a}{{{b^2} + a}} \ge 1 \Rightarrow P \le 1$

Dấu đẳng thức xảy ra khi và chỉ khi $a = b = 1$.

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Tiếng Anh

Giáo dục Kinh tế và Pháp luật

ĐHQG Hồ Chí Minh

ĐH Bách Khoa

ĐHQG Hà Nội

Bộ Công an

ĐHSP Hà Nội

Bằng lái xe

English Test

IT Test

Đại học

Viên chức

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Tin học

Giáo dục Kinh tế và Pháp luật

Global success

iLearn Smart World

Friends Global

Explore new worlds

Bright

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý