Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Ta có bảng giá trị sau
|
\[x\] |
\[ - 2\] |
\[ - 1\] |
\[0\] |
\[1\] |
\[2\] |
|
\[y = - {x^2}\] |
\[ - 4\] |
\[ - 1\] |
\[0\] |
\[ - 1\] |
\[ - 4\] |
|
\[y = x - 2\] |
\[ - 4\] |
\[ - 3\] |
\[ - 2\] |
\[ - 1\] |
\[0\] |
Đồ thị hàm số của \[\left( P \right)\] qua các điểm: \[( - 2; - 4)\], \[( - 1; - 1)\], \[(0;0)\], \[(1; - 1)\], \[(2; - 4)\].
Đồ thị hàm số của \[(d)\] qua các điểm: \[( - 2; - 4)\], \[( - 1; - 3)\], \[(0; - 2)\], \[(1; - 1)\], \[(2;0)\].
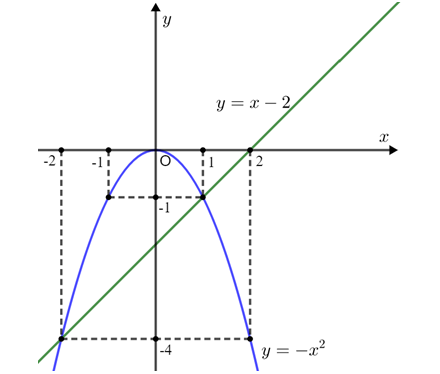
b) Phương trình hoành độ giao điểm của \[\left( P \right)\] và \[\left( d \right)\] là:
\[ - {x^2} = x - 2\] \[ \Leftrightarrow \] \[{x^2} + x - 2 = 0\]
\[ \Leftrightarrow \left[ \begin{array}{l}{x_1} = 1\\{x_2} = - 2\end{array} \right.\] \[ \Rightarrow \left[ \begin{array}{l}{y_1} = - 1\\{y_2} = - 4\end{array} \right.\].
Vậy \[\left( P \right)\] và \[\left( d \right)\] hai giao điểm là \[(1; - 1)\] và \[( - 2; - 4)\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi \[x\] (ngày) là số ngày nghỉ dự định của gia đình An tại Nha Trang (\[x > 0\]).
Vì gia đình An dự định đi du lịch tại Nha Trang và Huế trong 7 ngày nên suy ra số ngày nghỉ dự định tại Huế là \[7 - x\] .
Theo đề bài, ta có chi phí gia đình An chi ở Nha Trang là \[2x\] triệu đồng, ở Huế là \[3.\left( {7 - x} \right)\] triệu đồng.
Chi phí toàn bộ chuyến đi là 18 triệu đồng nên ta có phương trình:
\[2x + 3.\left( {7 - x} \right) = 18\]
\[ \Leftrightarrow 2x + 21 - 3x = 18\]
\[ \Rightarrow x = 3\]
Vậy số ngày nghỉ dự định của gia đình An tại Nha Trang là 3 ngày, tại Huế là 4 ngày.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
![Cho đường tròn (O) tâm \[O\] bán kính \[R\] và điểm nằm ngoài đường tròn. Các tiếp (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/12/blobid3-1766922884.png)
![Cho đường tròn (O) tâm \[O\] bán kính \[R\] và điểm nằm ngoài đường tròn. Các tiếp (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2025/12/blobid4-1766922900.png)
![Cho đường tròn (O) tâm \[O\] bán kính \[R\] và điểm nằm ngoài đường tròn. Các tiếp (ảnh 3)](https://video.vietjack.com/upload2/quiz_source1/2025/12/blobid5-1766922911.png)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập