Cho hai hàm số \[y = \frac{1}{2}{x^2}\]và y = ax + b.
a) Tìm các hệ số a, b biết đường thẳng y = ax + b đi qua hai điểm M(-2; 2) và N(4; -1).
b) Với các giá trị a, b vừa tìm được hãy:
- Tìm giao điểm của đường thẳng y = ax + b với đồ thị hàm số \[y = \frac{1}{2}{x^2}\]bằng phương pháp đại số.
- Vẽ đồ thị của hàm số \[y = \frac{1}{2}{x^2}\]và đường thẳng y = ax + b trên cùng một mặt phẳng tọa độ.
Cho hai hàm số \[y = \frac{1}{2}{x^2}\]và y = ax + b.
a) Tìm các hệ số a, b biết đường thẳng y = ax + b đi qua hai điểm M(-2; 2) và N(4; -1).
b) Với các giá trị a, b vừa tìm được hãy:
- Tìm giao điểm của đường thẳng y = ax + b với đồ thị hàm số \[y = \frac{1}{2}{x^2}\]bằng phương pháp đại số.
- Vẽ đồ thị của hàm số \[y = \frac{1}{2}{x^2}\]và đường thẳng y = ax + b trên cùng một mặt phẳng tọa độ.
Quảng cáo
Trả lời:
a) Tìm các hệ số a, b biết đường thẳng y = ax + b đi qua hai điểm M(-2; 2) và N(4; -1).
+ Vì d đi qua điểm M(-2; 2) nên ta có: -2a + b=2 (1)
+ Vì d đi qua điểm N(4; -1) nên ta có: 4a + b = -1 (2)
Từ (1) và (2) ta có: \[\left\{ \begin{array}{l} - 2a + b = 2\\4a + b = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 6a = 3\\4a + b = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - \frac{1}{2}\\b = 1\end{array} \right.\]
Từ đó ta có đường thẳng (d): y= \[ - \frac{1}{2}\]x+1
- Xét PT hoành độ giao điểm của đường thẳng y = ax + b với đồ thị hàm số \[y = \frac{1}{2}{x^2}\]: \[\frac{1}{2}{x^2}\]\[ = - \frac{1}{2}\]x+1
\[ \Leftrightarrow {x^2} + x - 2 = 0\]
PT (1) có: a + b +c =0 nên có hai nghiệm: \[{x_1} = 1;{x_2} = - 2\]
Suy ra giá trị y tương ứng là: \[{y_1} = \frac{1}{2};{y_2} = 2\]
Vậy giao điểm của đường thẳng y = ax + b với đồ thị hàm số \[y = \frac{1}{2}{x^2}\]là P(1; \[\frac{1}{2}\]); M(-2; 2)
- HS vẽ đúng đồ thị
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
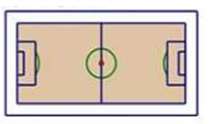
Gọi chiều dài, chiều rộng của khu đất lần lượt là x, y (m). Điều kiện x>y>4)
Diện tích của khu đất là xy (m2)
Chiều dài, chiều rộng của sân bóng đá lần lượt là x -4, y -4 (m) nên diện tích của sân bóng đá là (x -4)(y -4) (m2)
Vì lối đi có diện tích là 224 m2 nên ta có: xy - (x -4)(y -4) = 224
\[ \Leftrightarrow x + y = 60\] mà \[\frac{x}{y} = \frac{2}{3} \Leftrightarrow x = \frac{2}{3}y\]
Nên \[\frac{2}{3}y + y = 60 \Leftrightarrow y = 36\]. Từ đó x = 24
Vậy kích thước của khu đất là dài 36m và rộng 24m.
Lời giải
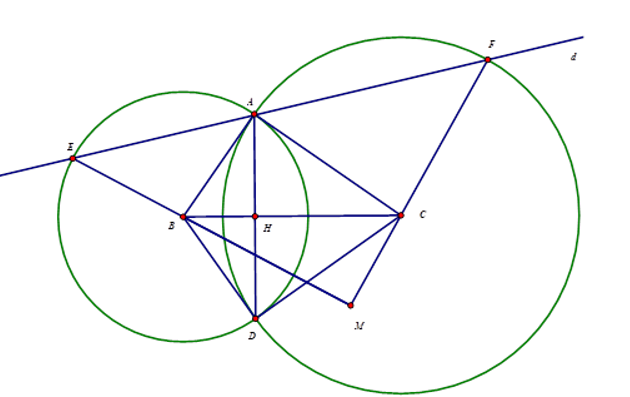
a)Vì tam giác ABC vuông tại A nên \[AB \bot AC\]từ đó có AB, AC lần lượt là tiếp tuyến của (C) và (B). Do đó: \[\widehat {BAC} = {90^0}\]
\[\Delta ABC = \Delta DBC(c.c.c)\] nên \[\widehat {BDC} = \widehat {BAC} = {90^0}\]
Suy ra: \[\widehat {BDC} + \widehat {BAC} = {180^0}\].
Vậy tứ giác ABDC nội tiếp được
b)Theo tính chất của hai đường tròn cắt nhau ta có BC là đường trung trực của AD và H là trung điểm của AD ( H là giao điểm của BC với AD)
Áp dụng hệ thức lượng trong tam giác vuông BAC ta có:
\[\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} \Leftrightarrow A{H^2} = \frac{{A{B^2}.A{C^2}}}{{A{B^2}.A{C^2}}} = \frac{{9.16}}{{25}}\]
\[ \Leftrightarrow AH = \frac{{12}}{5} = 2,4\]cm. Suy ra AD = 4,8 cm.
c)\[\Delta ABE\] cân tại B nên \[\widehat {BEA} = \widehat {BAE}\];
\[\Delta ACF\] cân tại C nên \[\widehat {C{\rm{AF}}} = \widehat {CFA}\] mà A, D, E thẳng hàng nên \[\widehat {BAE} + \widehat {C{\rm{AF}}} = {180^0} - \widehat {{\rm{BAC}}} = {90^0}\], suy ra: \[\widehat {BEA} + \widehat {CF{\rm{A}}} = {90^0}\]
Hay \[\widehat {MEF} + \widehat {MFE} = {90^0}\]suy ra \[\Delta M{\rm{EF}}\] vuông tại M
Do đó: \[\widehat {BMC} = {90^0}\]
Suy ra M thuộc đường tròn đường kính BC cố định.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.