Một khu đất hình chữ nhật có tỉ số hai kích thước là \[\frac{2}{3}\]. Người ta làm một sân bóng đá mini 5 người ở giữa, chừa lối đi xung quanh (lối đi thuộc khu đất). Lối đi rộng 2m và có diện tích 224 m2. Tính kích thước của khu đất.

Chọn C

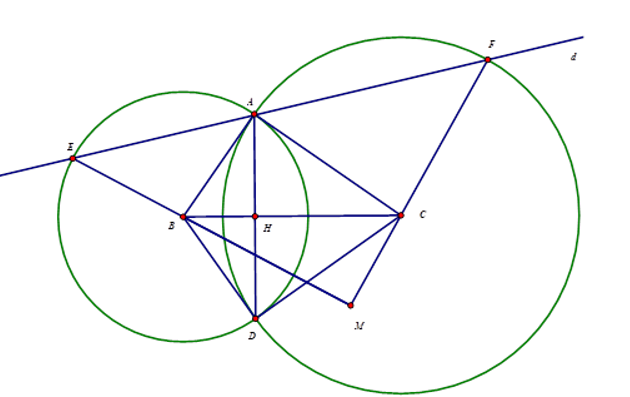
a)Vì tam giác ABC vuông tại A nên \[AB \bot AC\]từ đó có AB, AC lần lượt là tiếp tuyến của (C) và (B). Do đó: \[\widehat {BAC} = {90^0}\]

\[\Delta ABC = \Delta DBC(c.c.c)\] nên  \[\widehat {BDC} = \widehat {BAC} = {90^0}\]

Suy ra: \[\widehat {BDC} + \widehat {BAC} = {180^0}\].

Vậy tứ giác ABDC nội tiếp được

b)Theo tính chất của hai đường tròn cắt nhau ta có BC là đường trung trực của AD và H là trung điểm của AD ( H là giao điểm của BC với AD)

Áp dụng hệ thức lượng trong tam giác vuông BAC ta có:

\[\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} \Leftrightarrow A{H^2} = \frac{{A{B^2}.A{C^2}}}{{A{B^2}.A{C^2}}} = \frac{{9.16}}{{25}}\]

\[ \Leftrightarrow AH = \frac{{12}}{5} = 2,4\]cm. Suy ra AD = 4,8 cm.

c)\[\Delta ABE\] cân tại B nên \[\widehat {BEA} = \widehat {BAE}\];

\[\Delta ACF\] cân tại C nên \[\widehat {C{\rm{AF}}} = \widehat {CFA}\] mà A, D, E thẳng hàng nên \[\widehat {BAE} + \widehat {C{\rm{AF}}} = {180^0} - \widehat {{\rm{BAC}}} = {90^0}\], suy ra: \[\widehat {BEA} + \widehat {CF{\rm{A}}} = {90^0}\]

Hay \[\widehat {MEF} + \widehat {MFE} = {90^0}\]suy ra \[\Delta M{\rm{EF}}\] vuông tại M

Do đó: \[\widehat {BMC} = {90^0}\]

Suy ra M thuộc đường tròn đường kính BC cố định.