PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng (Đ) hoặc sai (S).
Cho hình chóp \[S.ABC\] có mặt bên \[\left( {SAB} \right)\] vuông góc với mặt đáy và tam giác \[SAB\] đều cạnh \[2a\]. Lấy \[H\] là trung điểm của \[AB\]. Biết tam giác \[ABC\] vuông tại \[C\] và cạnh \[AC = a\sqrt 3 \] . Khi đó:
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng (Đ) hoặc sai (S).
Cho hình chóp \[S.ABC\] có mặt bên \[\left( {SAB} \right)\] vuông góc với mặt đáy và tam giác \[SAB\] đều cạnh \[2a\]. Lấy \[H\] là trung điểm của \[AB\]. Biết tam giác \[ABC\] vuông tại \[C\] và cạnh \[AC = a\sqrt 3 \] . Khi đó:Quảng cáo
Trả lời:
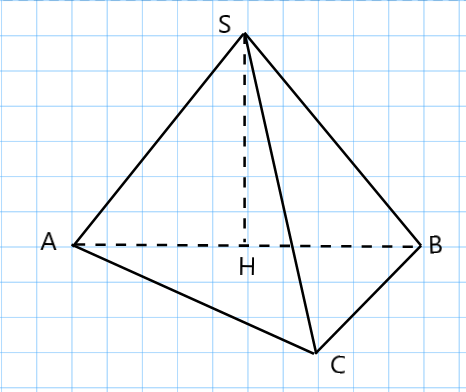
a) [NB] Trong tam giác đều \[SAB\],\[SH\]là đường cao. Do đó \[SH \bot AB\]
Theo giả thiết mặt bên \[(SAB) \bot (ABC)\], \[(SAB) \cap (ABC) = AB\], \[SH \subset (SAB)\] nên \[SH \bot (ABC)\]
a) đúng.
b) [TH] Giả sử \[\left( {SHC} \right) \bot \left( {SAC} \right)\].
Kẻ \[HK \bot SC\] tại \[K\]. Vì \[(SHC) \cap (SAC) = SC\] và \[HK \subset (SHC)\] nên \[HK \bot (SAC)\], suy ra \[HK \bot AC\].
Hơn nữa vì \[SH \bot (ABC)\] nên \[SH \bot AC\]. Suy ra \[AC \bot (SHC)\], suy ra \[AC \bot HC\]: điều này vô lý vì tam giác \[ABC\] vuông tại \[C\].
Vậy \[\left( {SHC} \right)\]không vuông góc với \[\left( {SAC} \right)\]
b) sai
c) \[(SAB) \bot (ABC)\]nên\[d(C,(SAB)) = d(C,AB) = \frac{{AC.BC}}{{AB}} = \frac{{a\sqrt 3 .\sqrt {4{a^2} - 3{a^2}} }}{{2a}} = \frac{{a\sqrt 3 }}{2}.\]
c) sai
d) Thể tích của khối chóp \[S.ABC\]là
\[V = \frac{1}{3}.{S_{\Delta ABC}}.SH = \frac{1}{3}.\frac{1}{2}.CA.CB.\frac{{AB\sqrt 3 }}{2} = \frac{{{a^3}}}{2}\].
d) sai
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: \(15\)
Từ giả thiết, điểm \(M\) thuộc mặt phẳng \(\left( P \right):x + 2y - z - 1 = 0\);
Có \(MA = MB\), suy ra \(M\) thuộc mặt phẳng trung trực của \(AB\)là \(\left( Q \right):y + z = 0\);
Suy ra\(M\)thuộc giao tuyến của hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\).
Ta tìm được đó là đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 1 - 3t\\y = t\\z = - t\end{array} \right.\).
Tham số hóa \(M\left( {1 - 3t;t; - t} \right)\) thì \(\overrightarrow {AM} \left( { - 1 - 3t;t - 2; - t} \right);\overrightarrow {BM} \left( { - 1 - 3t;t; - t + 2} \right)\)
Suy ra \(\cos AMB = \frac{{\overrightarrow {MA} .\overrightarrow {MB} }}{{MA.MB}} = \frac{{{{\left( {1 + 3t} \right)}^2} + t\left( {t - 2} \right).2}}{{{{\left( {1 + 3t} \right)}^2} + {{\left( {t - 2} \right)}^2} + {t^2}}} = \frac{{11{t^2} + 2t + 1}}{{11{t^2} + 2t + 5}} = f\left( t \right)\)
Để góc \(AMB\) lớn nhất thì ta cần \[\cos AMB = f\left( t \right)\] nhỏ nhất.
Khảo sát hàm \(f\left( t \right)\)ta được \(f\left( t \right)\)nhỏ nhất khi và chỉ khi \(t = - \frac{1}{{11}}\).
Suy ra \(M\left( {\frac{{14}}{{11}}; - \frac{1}{{11}};\frac{1}{{11}}} \right)\). Vậy \(S = 15\).
Câu 2
Lời giải
Hàm số dân số là \(f\left( t \right) = \frac{{26t + 10}}{{t + 5}}\) (nghìn người).
a) Số dân vào đầu năm 1980
Thời gian \(t\) tính từ năm 1970.
Năm 1980 ứng với \(t = 1980 - 1970 = 10\) (năm).
\[f\left( {10} \right) = \frac{{26 \cdot 10 + 10}}{{10 + 5}} = 18\]
Vậy số dân vào đầu năm 1980 là 18 nghìn người. Khẳng định a) đúng.
b) Số dân vào đầu năm 1995
Thời gian \(t\) tính từ năm 1970.
Năm 1995 ứng với \(t = 1995 - 1970 = 25\) (năm).
\[f\left( {25} \right) = \frac{{26 \cdot 25 + 10}}{{25 + 5}} = 22\].
Vậy số dân vào đầu năm 1995 là 22 nghìn người. Khẳng định b) sai
c) Xét tính đồng biến của hàm số \(f\left( t \right) = \frac{{26t + 10}}{{t + 5}}\).
\[f'\left( t \right) = \frac{{120}}{{{{\left( {t + 5} \right)}^2}}} > 0\], với mọi \(t \in [0, + \infty )\)
Vậy hàm số \(f\left( t \right)\) đồng biến trên \([0, + \infty )\). Khẳng định c) đúng.
d) Tốc độ tăng dân số vào năm 1998
Năm 1998 ứng với \(t = 1998 - 1970 = 28\) (năm).
\[f'\left( {28} \right) = \frac{{120}}{{{{\left( {28 + 5} \right)}^2}}} \approx 0,11019\] (nghìn người/năm).
Khẳng định d) sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.