Một cửa hàng bán tạp chí với giá 20 nghìn đồng một cuốn. Chi phí xuất bản \[x\]cuốn tạp chí (bao gồm: lương cán bộ, công nhân viên, giấy in,.) được cho bởi công thức\(C\left( x \right) = 0,0001{x^2} - 0,2x + 10000\), \(C\left( x \right)\) được tính theo đơn vị vạn đồng. Chi phí phát hành cho mỗi cuốn là 4 nghìn đồng. Các khoản thu bao gồm: tiền bán tạp chí và 90 triệu đồng trợ cấp cho báo chí. Giả sử số cuốn in ra đều được bán hết.Xét tính đúng sai của các mệnh đề sau:
Quảng cáo
Trả lời:
Lời giải
a) Ta có:
* Chi phí xuất bản \[x\]cuốn tạp chí là \(C\left( x \right)\): \(C\left( x \right) = 0,0001{x^2} - 0,2x + 10000\) (vạn đồng).
* Chi phí phát hành\[x\]cuốn tạp chí là \(H\left( x \right)\): \(H\left( x \right) = 0,4x\) (vạn đồng).
Tổng chi phí \(T\left( x \right)\) (xuất bản và phát hành) cho \(x\) cuốn tạp chí là
\(T\left( x \right) = C\left( x \right) + H\left( x \right)\)
\(T\left( x \right) = \left( {0,0001{x^2} - 0,2x + 10000} \right) + 0,4x\)
\(T\left( x \right) = 0,0001{x^2} + 0,2x + 10000\) vạn đồng.
Mệnh đề a) là ĐÚNG.
b) Số tiền lãi \(L\left( x \right)\) khi in \(x\) cuốn tạp chí bằng Tổng số tiền doanh thu trừ đi tổng số tiền chi phí
Ta tìm hàm doanh thu:
Giá bán \(20\) nghìn đồng/cuốn \( = 2\) vạn đồng/cuốn.
Doanh thu từ bán \(x\) cuốn: \(2x\) (vạn đồng).
Khoản trợ giúp: \(90\) triệu đồng \( = 9000\) vạn đồng.
Tổng doanh thu \(R\left( x \right)\) là: \(R\left( x \right) = 2x + 9000\) (vạn đồng)
Số tiền lãi \(L\left( x \right)\) khi in \(x\) cuốn tạp chí là \(L\left( x \right) = R\left( x \right) - T\left( x \right)\)
\(L\left( x \right) = \left( {2x + 9000} \right) - \left( {0,0001{x^2} + 0,2x + 10000} \right)\)
\(L\left( x \right) = - 0,0001{x^2} + \left( {2 - 0,2} \right)x + \left( {9000 - 10000} \right)\)
\(L\left( x \right) = - 0,0001{x^2} + 1,8x - 1000\)
Mệnh đề b) là SAI
c) Để có lãi cần in bao nhiêu cuốn
Để có lãi, ta cần \(L\left( x \right) > 0\).
\( - 0,0001{x^2} + 1,8x - 1000 > 0 \Leftrightarrow \)\(573,85 < x < 17426.14\)
Vậy, để có lãi (in ra số nguyên cuốn), cần in từ \(574\) đến \(17426\) cuốn.
Mệnh đề c) là ĐÚNG
d) Hàm lãi \(L\left( x \right) = - 0,0001{x^2} + 1,8x - 1000\) là một parabol có hệ số \(a = - 0,0001 < 0\), nên hàm số đạt giá trị lớn nhất tại đỉnh của parabol.
\({x_{{\rm{max}}}} = - \frac{b}{{2a}} = - \frac{{1,8}}{{ - 0,0002}} = 9000\)
Lãi lớn nhất đạt được khi in \(9000\) cuốn.
Mệnh đề d) là SAI.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
Đáp án: 0,75
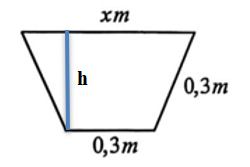
Ta có \(0 < x < 0,9\). Gọi \(h\) là chiều cao của hình thang cân ta có \(h = \sqrt {0,{3^2} - {{\left( {\frac{x}{2} - \frac{{0,3}}{2}} \right)}^2}} = \frac{{\sqrt { - 100{x^2} + 60x + 27} }}{{20}}\)
Diện tích đáy là
\[S\left( x \right) = \frac{1}{2}\left( {0,3 + x} \right)\frac{{\sqrt { - 100{x^2} + 60x + 27} }}{{20}} = \frac{1}{{400}}\left( {3 + 10x} \right)\sqrt { - 100{x^2} + 60x + 27} \].
\[\begin{array}{l}S'\left( x \right) = \frac{1}{{400}}\left[ {10\sqrt { - 100{x^2} + 60x + 27} + \left( {3 + 10x} \right)\frac{{ - 200x + 60}}{{2\sqrt { - 100{x^2} + 60x + 27} }}} \right]\\ = \frac{1}{{40}}\left[ {\frac{{ - 100{x^2} + 60x + 27 + \left( {3 + 10x} \right)\left( { - 10x + 3} \right)}}{{\sqrt { - 100{x^2} + 60x + 27} }}} \right] = \frac{{ - 200{x^2} + 60x + 36}}{{40\sqrt { - 100{x^2} + 60x + 27} }}\\S'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 0,15\\x = 0,75\end{array} \right.\end{array}\]
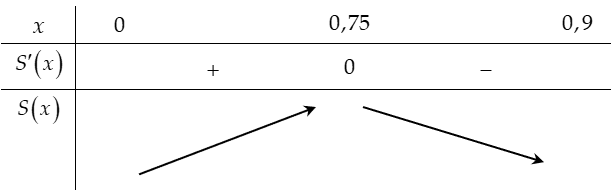
Do chiều cao của máng là 3 m không đổi suy ra thể tích máng lớn nhất khi diện tích đáy lớn nhất.
Vậy \(x = 0,75\left( m \right)\) thì thể tích máng xối lớn nhất.
Lời giải
Lời giải
Đáp án: 15.
Ta có \(\overrightarrow {AB} \) cùng phương với \(\overrightarrow u \left( {2; - 2;1} \right)\)nên \(\frac{{540}}{2} = \frac{{{y_B} - 3}}{{ - 2}} = \frac{{{z_B}}}{1} \Leftrightarrow \left\{ \begin{array}{l}{y_B} = - 537\\{z_B} = 270\end{array} \right.\)\( \Rightarrow B\left( {550; - 537;270} \right)\)
Quãng đường \(AB = 810m\) thì cabin di chuyển hết 3 phút. Vậy để cabin di chuyển hết quãng đường \(AD = 4050m\) thì mất \(\frac{{4050}}{{810}}.3 = 15\) phút.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
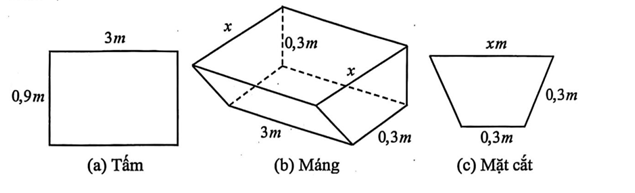
![Lời giải Chọn D Từ đồ thị ta có giá trị lớn nhất của hàm số trên \(\left[ { - 1;3} \right]\) bằng \(3\). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/12/4-1766978932.png)