Trong không gian \[Oxyz\], cho hai điểm \[A\left( {0;0; - 2} \right)\]và \[B\left( {2; - 2;1} \right)\]. Các mệnh đề sau là đúng hay sai?
Quảng cáo
Trả lời:
Lời giải
a) Đúng: Ta có \[\overrightarrow {AB} = \left( {2; - 2;3} \right)\].
b) Sai: Ta có \[\overrightarrow {OB} = 2\overrightarrow i - 2\overrightarrow j + \overrightarrow k \]
c) Đúng: Gọi \[D\left( {x;y;z} \right)\], vì \[ABOD\] hình bình hành nên \[\overrightarrow {AB} = \overrightarrow {DO} \].
\[ \Leftrightarrow \left\{ \begin{array}{l} - x = 2\\ - y = - 2\\ - z = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 2\\y = 2\\z = - 3\end{array} \right.\].
Vậy \[D\left( { - 2;2; - 3} \right)\].
d) Đúng: Vì điểm \[E\] thuộc tia \[Ox\] nên \[E\left( {x;0;0} \right),\,x > 0\].
Do đó \[\overrightarrow {OE} = \left( {x;0;0} \right) \Leftrightarrow OE = \left| x \right| = 3 \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = - 3\end{array} \right.\]. Vì \(x > 0\) nên \(x = - 3\) loại.
Vậy \[E\left( {3;0;0} \right)\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Lời giải
a) Ta có:
* Chi phí xuất bản \[x\]cuốn tạp chí là \(C\left( x \right)\): \(C\left( x \right) = 0,0001{x^2} - 0,2x + 10000\) (vạn đồng).
* Chi phí phát hành\[x\]cuốn tạp chí là \(H\left( x \right)\): \(H\left( x \right) = 0,4x\) (vạn đồng).
Tổng chi phí \(T\left( x \right)\) (xuất bản và phát hành) cho \(x\) cuốn tạp chí là
\(T\left( x \right) = C\left( x \right) + H\left( x \right)\)
\(T\left( x \right) = \left( {0,0001{x^2} - 0,2x + 10000} \right) + 0,4x\)
\(T\left( x \right) = 0,0001{x^2} + 0,2x + 10000\) vạn đồng.
Mệnh đề a) là ĐÚNG.
b) Số tiền lãi \(L\left( x \right)\) khi in \(x\) cuốn tạp chí bằng Tổng số tiền doanh thu trừ đi tổng số tiền chi phí
Ta tìm hàm doanh thu:
Giá bán \(20\) nghìn đồng/cuốn \( = 2\) vạn đồng/cuốn.
Doanh thu từ bán \(x\) cuốn: \(2x\) (vạn đồng).
Khoản trợ giúp: \(90\) triệu đồng \( = 9000\) vạn đồng.
Tổng doanh thu \(R\left( x \right)\) là: \(R\left( x \right) = 2x + 9000\) (vạn đồng)
Số tiền lãi \(L\left( x \right)\) khi in \(x\) cuốn tạp chí là \(L\left( x \right) = R\left( x \right) - T\left( x \right)\)
\(L\left( x \right) = \left( {2x + 9000} \right) - \left( {0,0001{x^2} + 0,2x + 10000} \right)\)
\(L\left( x \right) = - 0,0001{x^2} + \left( {2 - 0,2} \right)x + \left( {9000 - 10000} \right)\)
\(L\left( x \right) = - 0,0001{x^2} + 1,8x - 1000\)
Mệnh đề b) là SAI
c) Để có lãi cần in bao nhiêu cuốn
Để có lãi, ta cần \(L\left( x \right) > 0\).
\( - 0,0001{x^2} + 1,8x - 1000 > 0 \Leftrightarrow \)\(573,85 < x < 17426.14\)
Vậy, để có lãi (in ra số nguyên cuốn), cần in từ \(574\) đến \(17426\) cuốn.
Mệnh đề c) là ĐÚNG
d) Hàm lãi \(L\left( x \right) = - 0,0001{x^2} + 1,8x - 1000\) là một parabol có hệ số \(a = - 0,0001 < 0\), nên hàm số đạt giá trị lớn nhất tại đỉnh của parabol.
\({x_{{\rm{max}}}} = - \frac{b}{{2a}} = - \frac{{1,8}}{{ - 0,0002}} = 9000\)
Lãi lớn nhất đạt được khi in \(9000\) cuốn.
Mệnh đề d) là SAI.
Lời giải
Lời giải
Đáp án: 0,75
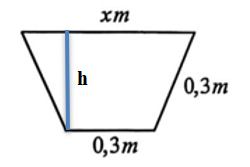
Ta có \(0 < x < 0,9\). Gọi \(h\) là chiều cao của hình thang cân ta có \(h = \sqrt {0,{3^2} - {{\left( {\frac{x}{2} - \frac{{0,3}}{2}} \right)}^2}} = \frac{{\sqrt { - 100{x^2} + 60x + 27} }}{{20}}\)
Diện tích đáy là
\[S\left( x \right) = \frac{1}{2}\left( {0,3 + x} \right)\frac{{\sqrt { - 100{x^2} + 60x + 27} }}{{20}} = \frac{1}{{400}}\left( {3 + 10x} \right)\sqrt { - 100{x^2} + 60x + 27} \].
\[\begin{array}{l}S'\left( x \right) = \frac{1}{{400}}\left[ {10\sqrt { - 100{x^2} + 60x + 27} + \left( {3 + 10x} \right)\frac{{ - 200x + 60}}{{2\sqrt { - 100{x^2} + 60x + 27} }}} \right]\\ = \frac{1}{{40}}\left[ {\frac{{ - 100{x^2} + 60x + 27 + \left( {3 + 10x} \right)\left( { - 10x + 3} \right)}}{{\sqrt { - 100{x^2} + 60x + 27} }}} \right] = \frac{{ - 200{x^2} + 60x + 36}}{{40\sqrt { - 100{x^2} + 60x + 27} }}\\S'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 0,15\\x = 0,75\end{array} \right.\end{array}\]
Do chiều cao của máng là 3 m không đổi suy ra thể tích máng lớn nhất khi diện tích đáy lớn nhất.
Vậy \(x = 0,75\left( m \right)\) thì thể tích máng xối lớn nhất.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
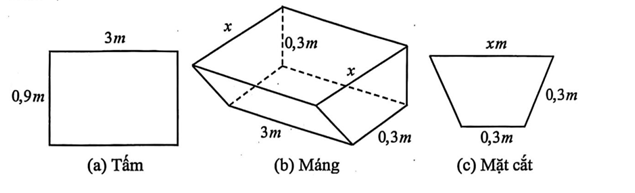
![Lời giải Chọn D Từ đồ thị ta có giá trị lớn nhất của hàm số trên \(\left[ { - 1;3} \right]\) bằng \(3\). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/12/4-1766978932.png)