Mảnh đất vườn của nhà anh Điệp có một phần ranh giới cũng là một phần đường cong (C):\(y = \frac{{x + a}}{{2x + b}}\), bao quanh nó là sông nước. Với hệ trục tọa độ Oxy thích hợp, đơn vị trên mỗi trục là 10 mét thì đường cong (C) đi qua điểm \(\left( {2\,;\,\,3} \right)\) và có đường tiệm cận đứng \(x = \frac{1}{2}\). Hàng ngày anh Điệp phải dùng thuyền máy để vận chuyển trái cây từ khu vườn của mình đến hai tuyến đường \({\Delta _1}:2x + y - 4 = 0\) và \({\Delta _2}:x + 2y - 2 = 0\) cho những người lái buôn từ nơi khác đến. Anh Điệp cần xác định một vị trí \(M\left( {{x_0}\,;\,\,{y_0}} \right)\) thuộc khu vườn của mình để tổng các khoảng cách từ vị trí M đó đến hai tuyến đường \({\Delta _1},\,\,{\Delta _2}\) là bé nhất. Hỏi khoảng cách từ vị trí được chọn làm gốc tọa độ đến điểm M là bao nhiêu mét ( làm tròn đến hàng phần chục)?
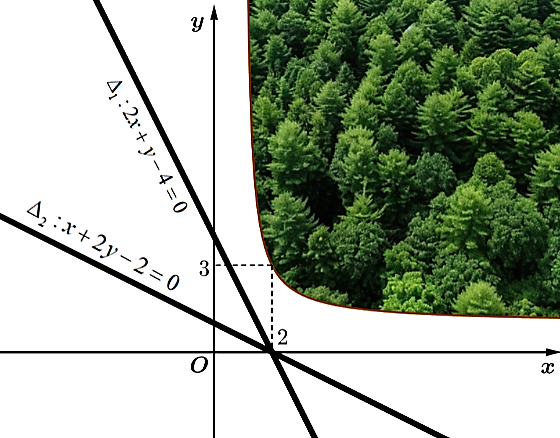
Mảnh đất vườn của nhà anh Điệp có một phần ranh giới cũng là một phần đường cong (C):\(y = \frac{{x + a}}{{2x + b}}\), bao quanh nó là sông nước. Với hệ trục tọa độ Oxy thích hợp, đơn vị trên mỗi trục là 10 mét thì đường cong (C) đi qua điểm \(\left( {2\,;\,\,3} \right)\) và có đường tiệm cận đứng \(x = \frac{1}{2}\). Hàng ngày anh Điệp phải dùng thuyền máy để vận chuyển trái cây từ khu vườn của mình đến hai tuyến đường \({\Delta _1}:2x + y - 4 = 0\) và \({\Delta _2}:x + 2y - 2 = 0\) cho những người lái buôn từ nơi khác đến. Anh Điệp cần xác định một vị trí \(M\left( {{x_0}\,;\,\,{y_0}} \right)\) thuộc khu vườn của mình để tổng các khoảng cách từ vị trí M đó đến hai tuyến đường \({\Delta _1},\,\,{\Delta _2}\) là bé nhất. Hỏi khoảng cách từ vị trí được chọn làm gốc tọa độ đến điểm M là bao nhiêu mét ( làm tròn đến hàng phần chục)?

Quảng cáo
Trả lời:
Đáp án:
Đáp án: 34,5
Đồ thị hàm số có tiệm cận đứng \(x = - \frac{b}{2} = \frac{1}{2} \Rightarrow b = - 1\).
Khi đó đồ thị hàm số \(y = \frac{{x + a}}{{2x - 1}}\) qua \(\left( {2\,;\,\,3} \right) \Rightarrow 3 = \frac{{2 + a}}{{2.2 - 1}} \Rightarrow a = 7\); hàm số là (C).
Ta nhận thấy để khoảng cách từ điểm M thuộc khu vườn đến hai đường thẳng là nhỏ nhất thì điểm M phải thuộc đồ thị hàm số.
Gọi \(M\left( {{x_0}\,;\,\,\frac{{{x_0} + 7}}{{2{x_0} - 1}}} \right) \in \left( C \right),\,\,{x_0} > \frac{1}{2}\). Tổng khoảng cách từ M đến hai đường thẳng \({\Delta _1},\,\,{\Delta _2}\) là
\(d = d\left( {M\,,\,\,{\Delta _1}} \right) + d\left( {M\,,\,\,{\Delta _2}} \right) = \frac{{\left| {2{x_0} + \frac{{{x_0} + 7}}{{2{x_0} - 1}} - 4} \right|}}{{\sqrt 5 }} + \frac{{\left| {{x_0} + 2 \cdot \frac{{{x_0} + 7}}{{2{x_0} - 1}} - 2} \right|}}{{\sqrt 5 }}\) ;
\(\sqrt 5 d = \left| {\frac{{4x_0^2 - 9{x_0} + 11}}{{2{x_0} - 1}}} \right| + \left| {\frac{{2x_0^2 - 3{x_0} + 16}}{{2{x_0} - 1}}} \right| = \frac{{4x_0^2 - 9{x_0} + 11}}{{2{x_0} - 1}} + \frac{{2x_0^2 - 3{x_0} + 16}}{{2{x_0} - 1}}\) (vì \(\left\{ \begin{array}{l}4x_0^2 - 9{x_0} + 11 > 0\\2{x_0} - 1 > 0\\2x_0^2 - 3{x_0} + 16 > 0\end{array} \right.\,,\,\,\forall {x_0} > \frac{1}{2}\)).
Đặt \(\sqrt 5 d = \frac{{6x_0^2 - 12{x_0} + 27}}{{2{x_0} - 1}} = g\left( x \right)\) với \({x_0} > \frac{1}{2}\).
Ta có: \(g'\left( x \right) = \frac{{12x_0^2 - 12{x_0} - 42}}{{{{\left( {2{x_0} - 1} \right)}^2}}}\); \(g'\left( x \right) = 0 \Rightarrow 12x_0^2 - 12{x_0} - 42 = 0 \Rightarrow {x_0} = \frac{{1 + \sqrt {15} }}{2} > \frac{1}{2}\).
Ta có: .
Dấu đẳng thức xảy ra khi \({x_0} = \frac{{1 + \sqrt {15} }}{2}\)\( \Rightarrow M\left( {\frac{{1 + \sqrt {15} }}{2}\,;\,\,\frac{{1 + \sqrt {15} }}{2}} \right)\).
Khoảng cách OM trên thực tế là mét.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
Đáp số : 5
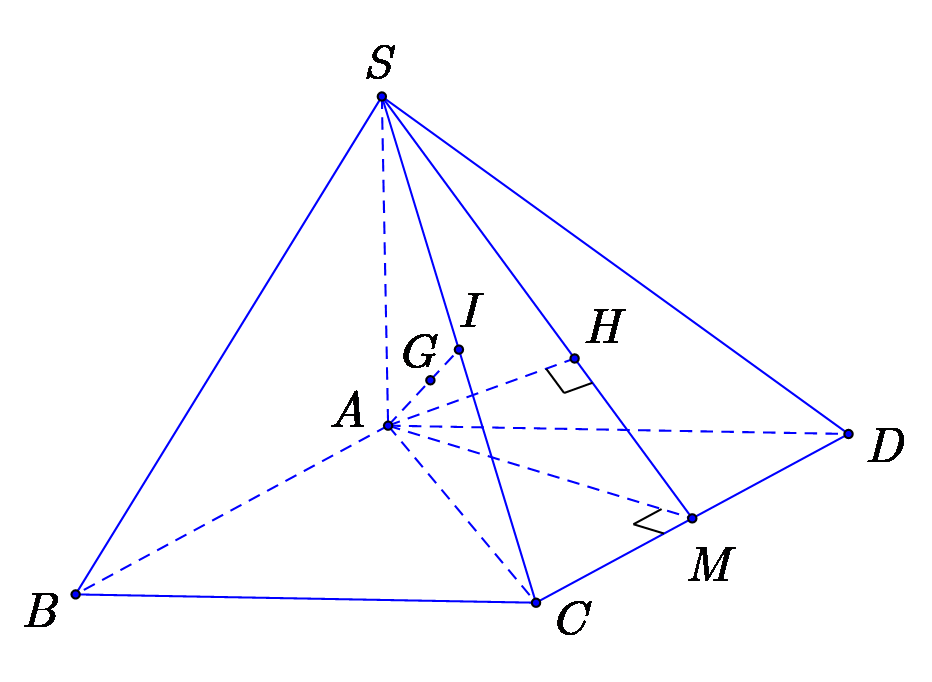
Gọi \(M,I\)lần lượt là trung điểm \(CD,\,SC\).
Theo giả thiết ta có tam giác \(ACD\) đều. Suy ra \(AM = \frac{{AD\sqrt 3 }}{2} = \sqrt 3 a\).
Kẻ \(AH \bot SM\,\,\left( {H \in SM} \right)\) thì \(AH \bot \left( {SCD} \right)\).
Ta có \(GI = \frac{1}{3}AI\) nên \(d\left( {G,\left( {SCD} \right)} \right) = \frac{1}{3}d\left( {A,\left( {SCD} \right)} \right) = \frac{1}{3}AH\)
\( = \frac{1}{3}.\frac{{AM.SA}}{{\sqrt {A{M^2} + S{A^2}} }} = \frac{1}{3}.\frac{{\sqrt 3 a.\sqrt 6 a}}{{\sqrt {3{a^2} + 6{a^2}} }} = \frac{{\sqrt 2 a}}{3}\)
Vậy \(d\left( {G,\left( {SCD} \right)} \right) = \frac{{\sqrt 2 a}}{3}\).
Câu 2
Lời giải
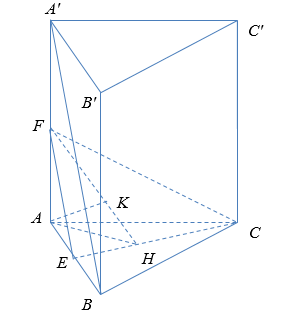
a) Sai.
b) Sai
Khoảng cách giữa hai đường thẳng \(A'B\) và \(CE\) bằng khoảng cách giữa A’B và (EFC)
\( \Rightarrow d(A'B,CE) = d(A'B,({\rm{EF}}C)) = d(B;({\rm{EF}}C)) = d(A;({\rm{EF}}C)) = AK\)
Với H là hình chiếu của A lên EC, K là hình chiếu của A lên FH.
\( \Rightarrow \frac{1}{{A{K^2}}} = \frac{1}{{A{C^2}}} + \frac{1}{{A{E^2}}} + \frac{1}{{{\rm{A}}{{\rm{F}}^2}}} = \frac{1}{9} + \frac{1}{1} + \frac{1}{4} = \frac{{49}}{{36}} \Rightarrow AK = \frac{6}{7}\).
c) Sai.
Tam giác ABC vuông tại A \( \Rightarrow AB = \sqrt {B{C^2} - A{B^2}} = \sqrt {13 - 4} = 3\)
\( \Rightarrow {V_{ltru}} = \frac{1}{2}.2.3.4 = 12\)
d) Đúng
Góc giữa đường thẳng \(A'B\) và mặt phẳng đáy \(\left( {ABC} \right)\) bằng A’BA
\( \Rightarrow \cos \widehat {A'BA} = \frac{{AB}}{{A'B}} = \frac{2}{{\sqrt {4 + 16} }} = \frac{1}{{\sqrt 5 }}\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Thống kê nhiệt độ tại một địa điểm trong 40 ngày, ta có bảng số liệu sau:
|
Nhiệt độ \(\left( {^\circ C} \right)\) |
\(\left[ {19;22} \right)\) |
\(\left[ {22;25} \right)\) |
\(\left[ {25;28} \right)\) |
\(\left[ {28;31} \right)\) |
|
Số ngày |
7 |
15 |
12 |
6 |
Nhiệt độ trung bình là?
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.