Cho khối lăng trụ \(ABC.A'B'C'\) có đáy là tam giác đều, \(A'A = A'B = A'C = a\sqrt 7 \) và \(B'C\) tạo với mặt phẳng \(\left( {ABC} \right)\) một góc \({30^ \circ }\). Thể tích của khối lăng trụ \(ABC.A'B'C'\) bằng:
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là D
Phương pháp giải
Tính thể tích
Lời giải
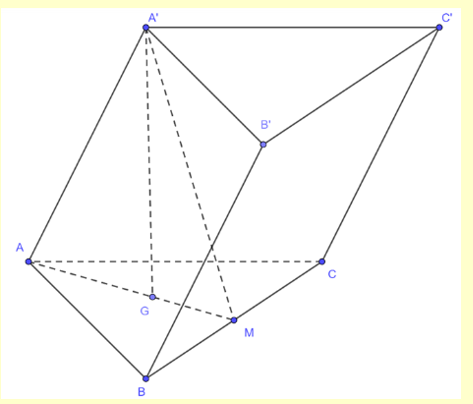
Ta có \(A'A = A'B = A'C = a\sqrt 7 \) nên \(A'\) cách đều ba điểm \(A,B,C\). Gọi \(M\) là trung điểm của \(BC\) và \(G\) là trọng tâm tam giác đều \(ABC\) suy ra \(A'G \bot \left( {ABC} \right)\)
Gọi \(H\) là hình chiếu của \(B'\) lên \(\left( {ABC} \right),B'C \cap \left( {ABC} \right) = C \Rightarrow HC\) là hình chiếu của \(B'C\) lên \(\left( {ABC} \right)\).
Suy ra \(\left( {B'C\widehat {\left( {ABC} \right)}} \right) = \left( {\widehat {B'C;HC}} \right) = {30^ \circ }\), và
\(B'H = d\left( {B';\left( {ABC} \right)} \right) = d\left( {A';\left( {ABC} \right)} \right) = A'G\) (vì \(A'B'//\left( {ABC} \right)\))
Xét tam giác \(B'HC\) vuông tại \(H\) ta có:
\({\rm{sin}}{30^ \circ } = \frac{{d\left( {B';\left( {ABC} \right)} \right)}}{{B'C}} = \frac{{d\left( {A';\left( {ABC} \right)} \right)}}{{B'C}} = \frac{{A'G}}{{B'C}}\).
Suy ra \(B'C = 2A'G\), đặt \(x = A'G,x > 0 \Rightarrow B'C = 2x\).
Mà ta thấy \(BC \bot \left( {A'AM} \right) \Rightarrow BC \bot A'A \Rightarrow BC \bot B'B \Rightarrow B'BC'C\) là hình chữ nhật.
Xét tam giác \(A'AG\) vuông tại \(G\), suy ra
\(AG = \sqrt {A'{A^2} - A'{G^2}} = \sqrt {7{a^2} - {x^2}} \Rightarrow AM = \frac{3}{2}AG = \frac{3}{2}\sqrt {7{a^2} - {x^2}} \)
\( \Rightarrow AB = BC = AC = \sqrt {3\left( {7{a^2} - {x^2}} \right)} \).
Xét tam giác \(B'BC\) vuông tại \(B\)
\( \Leftrightarrow B'{B^2} + B{C^2} = B'{C^2} \Leftrightarrow 7{a^2} + 3\left( {7{a^2} - {x^2}} \right) = 4{x^2} \Leftrightarrow x = 2a\).
Suy ra \(A'G = 2a \Rightarrow AB = BC = AC = 3a \Rightarrow {S_{ABC}} = \frac{{9\sqrt 3 }}{4}{a^2}\).
Vậy \({V_{ABC.A'B'C'}} = A'G.{S_{ABC}} = 2a.\frac{{9\sqrt 3 }}{4}{a^2} = \frac{{9\sqrt 3 }}{2}{a^3}\).
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là "2"
Phương pháp giải
Sử dụng tam giác đồng dạng.
Lời giải
Ta chọn mặt phẳng chứa \(AD\) là \(\left( {ACD} \right)\).
\(M\) là điểm chung của hai mặt phẳng \(\left( {ACD} \right)\) và \(\left( {MNP} \right)\).
Gọi \(CD\) cắt \(NP\) tại \(I\) nên \(\left( {ACD} \right) \cap \left( {MNP} \right) = MI\)
Gọi \(MI\) cắt \(AD\) tại \(F\) thì \(AD \cap \left( {MNP} \right) = F\).
Từ \(D\) kẻ đường thẳng song song với \(AC\) cắt \(MI\) tại \(E\)
Ta có \(\Delta DFE\) đồng dạng với \(\Delta AFM\) nên ta có \(\frac{{FA}}{{FD}} = \frac{{AM}}{{DE}} = \frac{{CM}}{{DE}}\) (1)
Ta có \(\Delta IED\) đồng dạng với \(\Delta IMC\) nên ta có \(\frac{{CM}}{{DE}} = \frac{{CI}}{{DI}}\) (2)
Từ \(D\) kẻ đường thẳng song song với \(CB\) cắt \(NI\) tại \(H\).
Ta có \(\Delta IHD\) đồng dạng với \(\Delta ICN\) nên ta có \(\frac{{CI}}{{DI}} = \frac{{CN}}{{DH}} = \frac{{NB}}{{DH}}\) (3)
Ta có \(\Delta NPB\) đồng dạng với \(\Delta HPD\) nên ta có \(\frac{{NP}}{{DH}} = \frac{{BP}}{{PD}} = 2\)
Từ (1), (2), (3) ta suy ra \(\frac{{FA}}{{FD}} = 2\)
Lời giải
Đáp án đúng là "1150"
Phương pháp giải
- Tính khối lượng aspirin trong 2,7 triệu viên nén.
- Tính khối lượng aspirin lý thuyết tổng hợp được để suy ra số mol salicylic acid cần dùng.
Lời giải
Số mol lý thuyết của aspirin được điều chế ra là: \(\frac{{{{500.10}^{ - 3}}.2,{{7.10}^6}}}{{180}}:90\% = \frac{{25000}}{3}\;{\rm{mol}}\)
Phản ứng xảy ra theo tỉ lệ mol 1 : 1 nên số mol salicylic acid cần dùng bằng số mol aspirin lý thuyết.
\( \Rightarrow {m_{{\rm{salicylic acid }}}} = \frac{{25000}}{3}.138 = 1150000{\rm{gam}} = 1150\;{\rm{kg}}\)
Vậy số cần điền là 1150.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập