Một chất điểm chuyển động theo quy luật vận tốc \(v\left( t \right)\left( {{\rm{m/s}}} \right)\) có dạng đường parapol khi \(0 \le t \le 4\) và có dạng đường thẳng khi \(4 \le t \le 9\). Cho đỉnh parapol là \(I\left( {2;1} \right)\). Hỏi quãng đường đi được của chất điểm trong thời gian \(0 \le t \le 10\left( s \right)\) là bao nhiêu mét?
Quảng cáo
Trả lời:
Đáp án đúng là D
Phương pháp giải
Ứng dụng của tích phân.
Lời giải
Gọi parapol \(\left( P \right):y = a{x^2} + bx + c\) khi \(0 \le t \le 4\)
Do \(\left( P \right)\) đi qua hai điểm \(I\left( {2;1} \right),A\left( {0;5} \right)\)
Suy ra \(\left\{ {\begin{array}{*{20}{l}}{4a + 2b + c = 1}\\{c = 5}\\{4a + b = 0}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = 1}\\{b = - 4}\\{c = 5}\end{array}} \right.} \right.\)
Quãng đường vật di chuyển trong khoảng thời gian \(0 \le t \le 4\) là \(S = \int\limits_0^4 {\left( {{x^2} - 4x + 5} \right)dx} = \frac{{28}}{3}\left( m \right)\)
Ta có \(f\left( 4 \right) = 5\)
Gọi đường thẳng \(d:y = ax + b\) khi \(4 \le t \le 9\) và \(d\) đi qua hai điểm \(B\left( {4;5} \right),C\left( {9;0} \right)\) nên
\(\left\{ {\begin{array}{*{20}{l}}{4a + b = 5}\\{9a + b = 0}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = - 1}\\{b = 9}\end{array}} \right.} \right.\)
Quãng đường vật di chuyển trong khoảng thời gian \(4 \le t \le 9\) là \(S = \int\limits_4^9 {\left( { - x + 9} \right)dx} = \frac{{25}}{2}\left( m \right)\)
Vậy tổng quãng đường chất điểm đi được trong thời gian \(0 \le t \le 9\) là \(S = \frac{{28}}{3} + \frac{{25}}{2} = \frac{{131}}{6}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là "10"
Phương pháp giải
- Thành phần trong đinh sắt gồm sắt nguyên chất và gỉ sắt và cả hai đều phản ứng với dung dịch H2SO4 loãng và đều chuyển hóa hoàn toàn về muối sắt sulfate vì H2SO4 dùng dư.
- Khi cho dung dịch BaCl2 dư vào thì dung dịch X thì có kết tủa BaSO4 được sinh ra.
- Nhỏ từ từ dung dịch KMnO4 0,02M vào 5,00 mL dung dịch X thì muối sắt(II) sulfate.
Lời giải
+) nBaSO4 = 0,0021 ⟹ nH2SO4 pư = 0,0021:2 = 0,00105
+) nKMnO4 = 1,8.10-4
2KMnO4 + 10.FeSO4 + 8.H2SO4 ⟶ 5.Fe2(SO4)3 + 2MnSO4 + K2SO4 + 8.H2O
1,8.10-4 ⟶ 9.10-4
+) BTNT S: nH2SO4 = nFeSO4 + 3.nFe2(SO4)3 ⟹ nFe2(SO4)3 = 5.10-5
⟹ nFe bị oxi hóa thành Fe2O3 = 2.5.10-5 = 10-4
⟹ ntổng số mol Fe = nFeSO4 + 2.nFe2(SO4)3 = 10-3
⟹ %Fe = (10-4/10-3).100% = 10%
Câu 2
Lời giải
Đáp án đúng là B
Phương pháp giải
Lời giải
Hiện tượng quan sát được khi cho vào propyne là thu được kết tủa vàng:
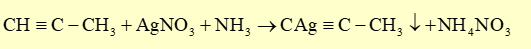
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
