Giải phương trình ta được họ nghiệm . Tính P = 2a+3b (nhập đáp án vào ô trống)
Đáp án: ___
Quảng cáo
Trả lời:
Đáp án đúng là "11"
Phương pháp giải
Giải phương trình lượng giác.
Lời giải
ĐКХĐ: \(\left\{ {\begin{array}{*{20}{l}}{{\rm{sin}}x \ne 0}\\{{\rm{cos}}x \ne 0}\end{array}} \right.\).
\(\frac{{2{\rm{sin}}x}}{{{\rm{cot}}x}} - \frac{{{\rm{tan}}x}}{{{\rm{sin}}x}} = 2\left( {{\rm{sin}}x - {\rm{cos}}x} \right) \Leftrightarrow 2{\rm{si}}{{\rm{n}}^2}x - {\rm{tan}}x{\rm{cot}}x\) \( = 2\left( {{\rm{sin}}x - {\rm{cos}}x} \right){\rm{sin}}x{\rm{cot}}x\)
\( \Leftrightarrow 2{\sin ^2}x - 1 = 2\left( {\sin x - \cos x} \right)\cos x \Leftrightarrow 2{\sin ^2}x - 1 = 2\sin x.{\rm{cos}}x - 2{\rm{co}}{{\rm{s}}^2}x\)
\( \Leftrightarrow 2{\rm{si}}{{\rm{n}}^2}x + 2{\rm{co}}{{\rm{s}}^2}x - 1 = {\rm{sin}}2x \Leftrightarrow {\rm{sin}}2x = 1 \Leftrightarrow 2x = \frac{\pi }{2} + k2\pi \Leftrightarrow x = \frac{\pi }{4} + k\pi \left( {k \in Z} \right)\)
Đối chiếu điều kiện, nghiệm phương trình là \(x = \frac{\pi }{4} + k\pi ,k \in Z\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = 4}\\{b = 1}\end{array} \Rightarrow P = 2a + 3b = 2.4 + 3.1 = 11} \right.\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là A
Phương pháp giải
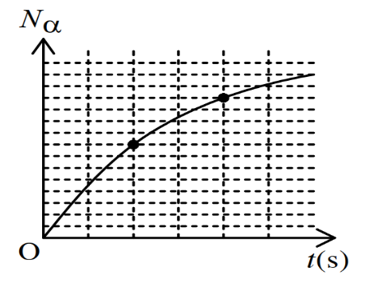
Sử dụng định luật phóng xạ về số hạt còn lại sau thời gian t: \(N = {N_0}{2^{ - \frac{t}{T}}}\)
Lời giải
Số hạt đã phân rã trong thời gian t:
\({N_\alpha } = {N_0}.\left( {1 - {2^{\frac{{ - t}}{T}}}} \right) \Rightarrow \left\{ {\begin{array}{*{20}{l}}{8\^o = {N_0}.\left( {1 - {2^{\frac{{ - 8}}{T}}}} \right)}\\{12\^o = {N_0}.\left( {1 - {2^{\frac{{ - 16}}{T}}}} \right)}\end{array} \Rightarrow \frac{8}{{12}}} \right. = \frac{{1 - {2^{\frac{{ - 8}}{T}}}}}{{1 - {2^{\frac{{ - 16}}{T}}}}} \Rightarrow T = 8s\)
Lời giải
Đáp án đúng là "5"
Phương pháp giải
Tính chất của tích phân.
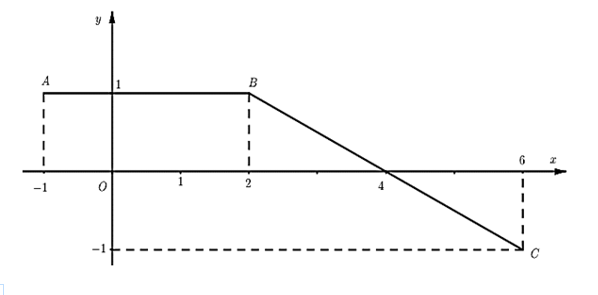
Lời giải
Từ đồ thị của hàm số ta xác định được \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{{\rm{1}}\,\,{\rm{khi}} - 1 \le x < 2}\\{ - \frac{1}{2}x + 2\,\,{\rm{khi}}\,\,2 \le x \le 6}\end{array}} \right.\).
Do \(F\) là nguyên hàm của \(f\) nên \(F\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{x + {C_1}\,\,{\rm{khi}}\,\, - 1 \le x < 2}\\{ - \frac{1}{4}{x^2} + 2x + {C_2}\,\,{\rm{khi}}\,\,2 \le x \le 6}\end{array}} \right.\).
Ta có \(F\left( { - 1} \right) = - 1 \Leftrightarrow - 1 + {C_1} = - 1 \Leftrightarrow {C_1} = 0\).
Hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;6} \right] \Rightarrow F\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;6} \right]\)
\( \Rightarrow F\left( x \right)\) liên tục tại \(x = 2\)
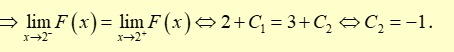
Suy ra \(F\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{x + {C_1}\,\,{\rm{khi}}\,\, - 1 \le x < 2}\\{ - \frac{1}{4}{x^2} + 2x - 1\,\,{\rm{khi}}\,\,2 \le x \le 6}\end{array}} \right.\). Vậy \(F\left( 4 \right) + F\left( 6 \right) = 5\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.