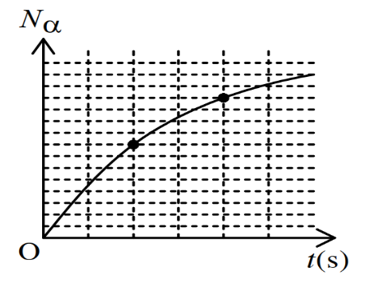
Hình vẽ biểu diễn số hạt α được phát ra từ một chất phóng xạ α theo thời gian t. Thang đo được sử dụng trong hình vẽ ứng với mỗi ô nằm ngang là 4s. Chu kì bán rã của chất phóng xạ là:

Đáp án đúng là "5"

Phương pháp giải

Tính chất của tích phân.

Lời giải

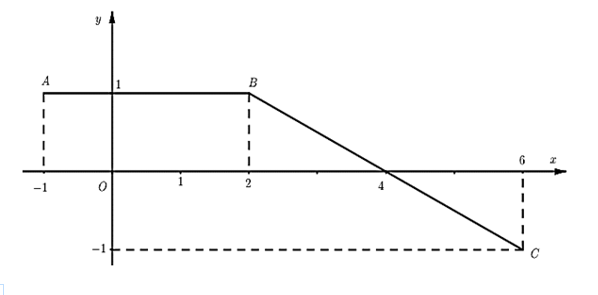
Từ đồ thị của hàm số ta xác định được \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{{\rm{1}}\,\,{\rm{khi}} - 1 \le x < 2}\\{ - \frac{1}{2}x + 2\,\,{\rm{khi}}\,\,2 \le x \le 6}\end{array}} \right.\).

Do \(F\) là nguyên hàm của \(f\) nên \(F\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{x + {C_1}\,\,{\rm{khi}}\,\, - 1 \le x < 2}\\{ - \frac{1}{4}{x^2} + 2x + {C_2}\,\,{\rm{khi}}\,\,2 \le x \le 6}\end{array}} \right.\).

Ta có \(F\left( { - 1} \right) =  - 1 \Leftrightarrow  - 1 + {C_1} =  - 1 \Leftrightarrow {C_1} = 0\).

Hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;6} \right] \Rightarrow F\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;6} \right]\)

\( \Rightarrow F\left( x \right)\) liên tục tại \(x = 2\)

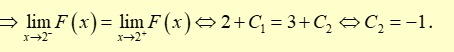
Suy ra \(F\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{x + {C_1}\,\,{\rm{khi}}\,\, - 1 \le x < 2}\\{ - \frac{1}{4}{x^2} + 2x - 1\,\,{\rm{khi}}\,\,2 \le x \le 6}\end{array}} \right.\). Vậy \(F\left( 4 \right) + F\left( 6 \right) = 5\).

Đáp án đúng là "5"

Phương pháp giải

Xác định đường tiệm cận

Lời giải

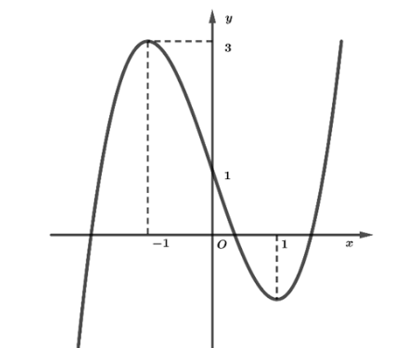
Ta có: \({f^2}\left( x \right) - 6f\left( x \right) + 8 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{f\left( x \right) = 3\,\,\,\left( 1 \right)}\\{f\left( x \right) = 1\,\,\,\left( 2 \right)}\end{array}} \right.\)

Dựa vào đồ thị hàm số, ta thấy:

(1) có nghiệm \({x_1} = a > 1\) (nghiệm đơn) và \({x_2} =  - 1\) (nghiệm kép) \( \Rightarrow f\left( x \right) - 3 = k\left( {x - a} \right){(x + 1)^2}(k > 0)\)

(2) có nghiệm ba nghiệm đơn \({x_1},{x_2},{x_3}\) với \({x_1} = b <  - 1 < {x_2} = 0 < 1 < {x_3} = c{\rm{\;}}(a > c)\)

\( \Rightarrow f\left( x \right) - 1 = k\left( {x - b} \right)x\left( {x - c} \right)(k > 0)\).

\( \Rightarrow \) Hàm số \(y = g\left( x \right)\) có tập xác định \(D = \mathbb{R}\backslash \left\{ {a;b;0;1;c} \right\}\)

Vì \(g\left( x \right) = \frac{{\left( {x + 1} \right)\left( {{x^2} - 1} \right)}}{{{f^2}\left( x \right) - 4f\left( x \right) + 3}} = \frac{{\left( {x + 1} \right)\left( {{x^2} - 1} \right)}}{{\left[ {f\left( x \right) - 3} \right]\left[ {f\left( x \right) - 1} \right]}} = \frac{{x - 1}}{{{k^2}x\left( {x - b} \right)\left( {x - c} \right)\left( {x - a} \right)}}\)

Nên  ĐTHS \(y = g\left( x \right)\) nhận đường thẳng \(y = 0\) làm TCN.

Tại các điểm \(x = a,x = b,x = 0,x = c\) mẫu của \(g\left( x \right)\) nhận giá trị bằng 0 còn tử nhận các giá trị khác 0.

Và do hàm số xác định trên \(D = \mathbb{R}\backslash \left\{ {a;b;0;1;c} \right\}\) nên giới hạn một bên của hàm số \(y = g\left( x \right)\) tại các điểm \(x = a,x = b,x = 0,x = 1,x = c\) là các giới hạn vô cực.

Do đó, ĐTHS \(y = g\left( x \right)\) có 4 TCĐ: \(x = a,x = b,x = 0\) và \(x = c\).                      

Vậy ĐTHS \(y = g\left( x \right)\) có 5 đường tiệm cận: \(1{\rm{\;}}\) TCN: \(y = 0\) và 4 TCĐ \(x = a,x = b,x = 0,x = c\).