Ông An có một thanh đá thạch anh màu xanh ngọc dạng hình lăng trụ đứng \(OAB.O'A'B'\), trong đó \(OA = OB = 2\,dm\), \(\widehat {AOB} = 120^\circ \), \(OO' = 4\,dm\). Ông mang thanh thạch anh này đến tiệm chuyên gia công và sản xuất đồ lưu niệm yêu cầu chủ tiệm phân chia thanh đá thành ba phần bởi hai mặt phẳng \(\left( {CAB} \right)\) và \(\left( {DAB} \right)\) sao cho tam giác \(CAB\) vuông, tamm giác \(DAB\) đều. Sau đó, làm một quả cầu pha lê ngoại tiếp khối thạch anh \(ABCD\) (\(4\) điểm \(A\), \(B\), \(C\), \(D\) thuộc mặt cầu, xem hình minh họa).

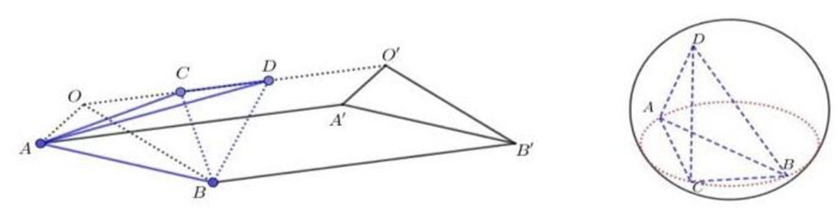
Chủ tiệm định giá tiền hoàn thành món hàng bằng bình phương thể tích khối thạch anh \(ABCD\) \(\left( {d{m^3}} \right)\) cộng với bình phương bán kính mặt cầu \(\left( {dm} \right)\) ngoại tiếp khối đó rồi nhân với \(60\) nghìn đồng \(\left( {\left( {V_{ABCD}^2 + {R^2}} \right).60\,000} \right)\). Hỏi ông An phải trả bao nhiêu nghìn đồng cho món đồ lưu niệm của mình?

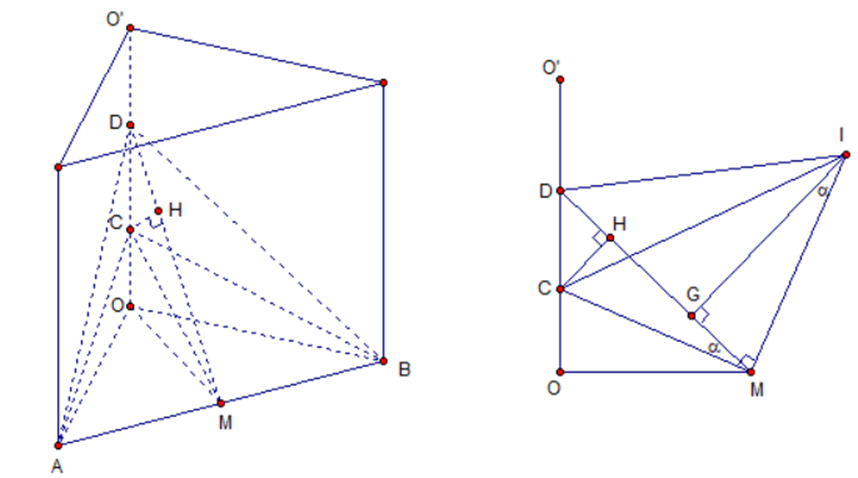
Ta có. \(AB = 2\sqrt 3 \), \(CA = CB = \frac{{AB}}{{\sqrt 2 }} = \sqrt 6 \), \(DA = DB = 2\sqrt 3 \), \(CM = \frac{1}{2}AB = \sqrt 3 \), \(DM = \frac{{AB\sqrt 3 }}{2} = 3\).

\({S_{\Delta OAB}} = \frac{1}{2}OA.OB.\sin 120^\circ  = \sqrt 3 \), \({S_{\Delta CAB}} = \frac{1}{2}CA.CB = 3\), \({S_{\Delta DAB}} = \frac{{{{\left( {2\sqrt 3 } \right)}^2}.\sqrt 3 }}{4} = 3\sqrt 3 \).

Gọi \(M\) là trung điểm của \(AB\), suy ra. \(AB \bot OM\),\(AB \bot CM\),\(AB \bot DM\).

Khi đó. \(\widehat {CMO} = \left( {\left( {OAB} \right),\left( {CAB} \right)} \right)\), \(\widehat {DMO} = \left( {\left( {DAB} \right),\left( {OAB} \right)} \right)\), \(\alpha  = \left( {\left( {CAB} \right),\left( {DAB} \right)} \right)\).

Vì \(\Delta OAB\) là hình chiếu của hai tam giác \(CAB\) và \(DAB\) trên mặt phẳng \(\left( {OAB} \right)\).

Ta có. \(\cos \widehat {CMO} = \frac{{{S_{\Delta OAB}}}}{{{S_{\Delta CAB}}}} = \frac{{\sqrt 3 }}{3}\)\( \Rightarrow \sin \widehat {CMO} = \frac{{\sqrt 6 }}{3}\),

\(\cos \widehat {DMO} = \frac{{{S_{\Delta OAB}}}}{{{S_{\Delta DAB}}}} = \frac{{\sqrt 3 }}{{3\sqrt 3 }} = \frac{1}{3}\)\( \Rightarrow \sin \widehat {DMO} = \frac{{2\sqrt 2 }}{3}\).

\(\cos \alpha  = \cos \left( {\widehat {DMO} - \widehat {CMO}} \right) = \cos \widehat {DMO}\cos \widehat {CMO} + \sin \widehat {DMO}\sin \widehat {CMO}\)

\( = \frac{{\sqrt 3 }}{3}.\frac{1}{3} + \frac{{\sqrt 6 }}{3}.\frac{{2\sqrt 2 }}{3} = \frac{{5\sqrt 3 }}{9}\).

\( \Rightarrow \sin \alpha  = \sqrt {1 - {{\left( {\frac{{5\sqrt 3 }}{9}} \right)}^2}} \)\( \Rightarrow \sin \alpha  = \sqrt {1 - {{\left( {\frac{{5\sqrt 3 }}{9}} \right)}^2}}  = \frac{{\sqrt 6 }}{9}\).

Từ \(C\) kẻ đường thẳng vuông góc với \(DM\) tại \(H\), suy ra.

\(\left\{ \begin{array}{l}CH \bot DM\\CH \bot AB\end{array} \right. \Rightarrow CH \bot \left( {ABD} \right) \Rightarrow CH\) là đường cao của tứ diện \(ABCD\).

Suy ra. \({V_{ABCD}} = \frac{1}{3}CH.{S_{\Delta DAB}} = \frac{1}{3}CM\sin \alpha .{S_{\Delta DAB}}\)\( = \frac{1}{3}.\sqrt 3 .\frac{{\sqrt 6 }}{9}.3\sqrt 3  = \frac{{\sqrt 6 }}{3}\)\( \Rightarrow V_{ABCD}^2 = \frac{2}{3}\).

Mặt khác, gọi \(I\) là tâm mặt cầu ngoại tiếp tứ diện \(ABCD\).

Điểm \(M\) là tâm đường tròn ngoại tiếp tam giác \(CAB\), suy ra. \(IM \bot \left( {ABC} \right) \Rightarrow IM \bot CM\).

Điểm \(G\) là tâm đường tròn ngoại tiếp tam giác \(DAB\), suy ra. \(IG \bot \left( {ABD} \right) \Rightarrow IG \bot DM\).

Và điểm \(G\) cũng là trọng tâm tam giác \(DAB\), \(GM = \frac{1}{3}DM = 1\).

Ta có. \(\widehat {GIM} + \widehat {GMI} = 90^\circ  = \widehat {GMI} + \widehat {GMC}\)\( \Rightarrow \widehat {GIM} = \widehat {GMC} = \alpha \).

Suy ra. \(GI = GM\cot \alpha  = \cot \alpha  = \frac{{5\sqrt 2 }}{2}\)\( \Rightarrow {R^2} = D{I^2} = D{G^2} + G{I^2} = {2^2} + {\left( {\frac{{5\sqrt 2 }}{2}} \right)^2} = \frac{{33}}{2}\).

Vậy số tiền ông An phải trả là \(\left( {\frac{2}{3} + \frac{{33}}{2}} \right).60\,\,000 = 1\,030\,\,000\) đồng.