Cho \(\widehat {xOy} = 70^\circ \). Trên tia \(Ox\) lấy điểm \(A\). Kẻ tia \(Az\) sao cho \(\widehat {xAz} = 70^\circ \) (Tia \(Az\) nằm trong \(\widehat {xOy}\)). Trên tia \(Az\) lấy điểm \(B\), kẻ tia \(Bt\) cắt \(Oy\) tại \(C\) sao cho \(\widehat {CBz} = 110^\circ \).
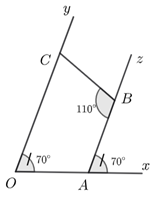
Khi đó:
Cho \(\widehat {xOy} = 70^\circ \). Trên tia \(Ox\) lấy điểm \(A\). Kẻ tia \(Az\) sao cho \(\widehat {xAz} = 70^\circ \) (Tia \(Az\) nằm trong \(\widehat {xOy}\)). Trên tia \(Az\) lấy điểm \(B\), kẻ tia \(Bt\) cắt \(Oy\) tại \(C\) sao cho \(\widehat {CBz} = 110^\circ \).
Khi đó:
a) \(\widehat {ABC}\) và \(\widehat {CBz}\) là hai góc kề bù.
Đúng
Sai
b) \(\widehat {CBz} = 70^\circ \).
Đúng
Sai
c) \(Oy\) song song với \(Az\).
Đúng
Sai
d) \(\widehat {BCO} = 110^\circ \).
Đúng
Sai
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Đúng.
Nhận thấy \(\widehat {ABC}\) và \(\widehat {CBz}\) là hai góc kề bù nên ta có \(\widehat {CBz} + \widehat {ABC} = 180^\circ \). Do đó, ý a) đúng.
b) Đúng.
Suy ra \(\widehat {CBz} = 180^\circ - \widehat {CBA} = 180^\circ - 110^\circ = 70^\circ \). Do đó, ý b) đúng.
Ta có \(\widehat {xAz} = \widehat {xOy} = 70^\circ \).
c) Đúng.
Mà hai góc ở vị trí đồng vị nên \(Oy\parallel Az\). Do đó, ý c) đúng.
d) Sai.
Vì \(Oy\parallel Az\) nên \(\widehat {OCB} = \widehat {CBz} = 70^\circ \) (so le trong). Do đó, ý d) sai.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
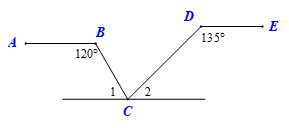
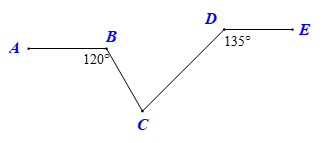
Kẻ đường thẳng qua \(C\) và song song với \[AB\].
Mà \(AB\,{\rm{//}}\,DE\) nên đường thẳng đó cũng song song với \[DE\].
Do đó \({\widehat C_1} + \widehat {ABC} = 180^\circ \) và \(\widehat {{C_2}} + \widehat {CDE} = 180^\circ \) (hai góc trong cùng phía)
Do đó, \[{\widehat C_1} = 60^\circ \] và \[\,{\widehat C_2} = 45^\circ \].
Suy ra \[\widehat {BCD} = 180^\circ - 60^\circ - 45^\circ = 75^\circ \].
Lời giải
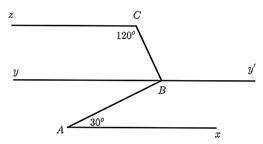
Ta có \(Ax\parallel Cz\) mà \(Ax\parallel yy'\) nên \(yy'\parallel Cz\).
Vì \(Ax\parallel yy'\) nên \(\widehat {BAx} = \widehat {ABy} = 30^\circ \)(so le trong)
Vì \(yy'\parallel Cz\) nên \(\widehat {zCB} = \widehat {CBy'} = 120^\circ \) (so le trong)
Ta có: \(\widehat {CBy'}\) và \(\widehat {CBy}\) là hai góc kề bù nên \(\widehat {CBy'} + \widehat {CBy} = 180^\circ \).
hay \(\widehat {CBy} = 180^\circ - \widehat {CBy'} = 180^\circ - 120^\circ = 60^\circ .\)
Lại có \(\widehat {CBy}\) và \(\widehat {ABy}\) là hai góc kề nhau nên \(\widehat {CBy} + \widehat {ABy} = \widehat {ABC}\).
Do đó, \(\widehat {ABC} = 30^\circ + 60^\circ = 90^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(\widehat {MAQ} = 150^\circ .\)
B. \(\widehat {MAQ} = 30^\circ .\)
C. \(\widehat {MAQ} = 180^\circ .\)
D. \(\widehat {MAQ} = 130^\circ .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Qua một điểm ở ngoài một đường thẳng, chỉ có một đường thẳng song song với đường thẳng đó.
B. Qua một điểm ở ngoài một đường thẳng, có vô số đường thẳng song song với đường thẳng đó.
C. Qua một điểm ở ngoài một đường thẳng, không kẻ được đường thẳng song song với đường thẳng đó.
D. Qua một điểm ở ngoài một đường thẳng, kẻ được ít nhất một đường thẳng song song với đường thẳng đó.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
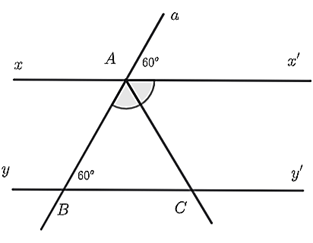
a) \(\widehat {aAx'}\) và \(\widehat {ABC}\) là hai góc so le trong.
Đúng
Sai
b) \(x'x\parallel yy'.\)
Đúng
Sai
c) \(\widehat {BAx'} = 120^\circ .\)
Đúng
Sai
d) \(AB\) là tia phân giác của \(\widehat {xAC}\).
Đúng
Sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập