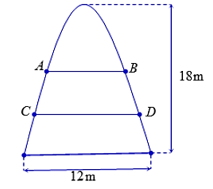
Một cổng chào có dạng hình Parabol chiều cao 18 m, chiều rộng tại chân cổng 12 m như hình vẽ bên. Người ta căng hai sợi dây trang trí AB,CD nằm ngang đồng thời chia hình giới hạn bởi Parabol và mặt đất thành ba phần có diện tích bằng nhau. Tỉ số bằng bao nhiêu (nhập đáp án vào ô trống, làm tròn kết quả đến hàng phần mười)?
Đáp án ____
Quảng cáo
Trả lời:
Giải bởi Vietjack
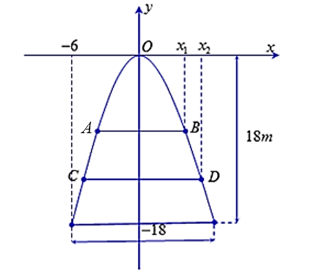
Chọn hệ trục tọa độ \(Oxy\) như hình vẽ bên.
Phương trình Parabol có dạng \(y = a{x^2}\,\,\,\left( P \right)\).
\(\left( P \right)\) đi qua điểm có tọa độ \(\left( { - 6; - 18} \right)\), suy ra \( - 18 = a \cdot {\left( { - 6} \right)^2}\)
\( \Leftrightarrow a = - \frac{1}{2} \Rightarrow \left( P \right):y = - \frac{1}{2}{x^2}\). Từ hình vẽ ta có: \(\frac{{AB}}{{CD}} = \frac{{{x_1}}}{{{x_2}}}\).
Diện tích hình phẳng giới hạn bởi Parabol và đường thẳng AB: \(y = - \frac{1}{2}x_1^2\) là:
\({S_1} = 2\int\limits_0^{{x_1}} {\left[ { - \frac{1}{2}{x^2} - \left( { - \frac{1}{2}x_1^2} \right)} \right]dx} = \left. {2\left( { - \frac{1}{2} \cdot \frac{{{x^3}}}{3} + \frac{1}{2}x_1^2 \cdot x} \right)} \right|_0^{{x_1}} = \frac{2}{3}x_1^3\).
Diện tích hình phẳng giới hạn bởi Parabol và đường thẳng CD: \(y = - \frac{1}{2}x_2^2\) là:
\({S_2} = 2\int\limits_0^{{x_2}} {\left[ { - \frac{1}{2}{x^2} - \left( { - \frac{1}{2}x_2^2} \right)} \right]dx} = \left. {2\left( { - \frac{1}{2} \cdot \frac{{{x^3}}}{3} + \frac{1}{2}x_2^2 \cdot x} \right)} \right|_0^{{x_2}} = \frac{2}{3}x_2^3\).
Từ giả thiết suy ra \({S_2} = 2{S_1} \Leftrightarrow x_2^3 = 2x_1^3 \Leftrightarrow \frac{{{x_1}}}{{{x_2}}} = \frac{1}{{\sqrt[3]{2}}}\). Vậy \(\frac{{AB}}{{CD}} = \frac{{{x_1}}}{{{x_2}}} = \frac{1}{{\sqrt[3]{2}}} \approx 0,8\).
Đáp án cần nhập là: \[0,8\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \[0,61\].
B. \[0,53\].
C. \[0,39\].
D. \[0,92\].
Lời giải
Gọi \(A\) là biến cố: “Chọn được một học sinh giỏi môn Tiếng Anh”, \(B\) là biến cố: “Chọn được một học sinh giỏi môn Toán”.
Xác suất để chọn được một học sinh giỏi Toán hoặc giỏi Anh là:
\(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right) = \frac{{12}}{{100}} + \frac{{35}}{{100}} - \frac{8}{{100}} = 0,39\).
Xác suất để chọn được một em học sinh không giỏi môn nào trong hai môn Toán, Tiếng Anh là: \(P\left( {\overline {A \cup B} } \right) = 1 - P\left( {A \cup B} \right) = 1 - 0,39 = 0,61\). Chọn A.
Câu 2
A. Cyberbullying involves spreading inaccurate, humiliating, or mean messages about someone online.
B. Cyberbullying is the act of sending kind and supportive messages through social media.
C. Cyberbullying means sharing friendly content about a person on digital platforms.
D. Cyberbullying is the practice of communicating factual, positive information about others on the internet.
Lời giải
Kiến thức về dạng Paraphrase của một câu
Dịch: Câu nào dưới đây diễn giải đúng nhất câu sau: “Cyberbullying is using digital media to communicate false, embarrassing, or unfriendly information about another person.”?
A. Bắt nạt trên mạng liên quan đến việc phát tán các thông điệp không chính xác, làm nhục hoặc có ác ý về ai đó trên mạng.
B. Bắt nạt trên mạng là hành vi gửi các thông điệp tử tế và khích lệ thông qua mạng xã hội.
C. Bắt nạt trên mạng có nghĩa là chia sẻ nội dung thân thiện về một người trên các nền tảng kỹ thuật số.
D. Bắt nạt trên mạng là hành vi truyền đạt thông tin thực tế, tích cực về người khác trên internet.
Thông tin: Cyberbullying is using digital media to communicate false, embarrassing, or unfriendly information about another person. (Bắt nạt trên mạng là sử dụng phương tiện kỹ thuật số để truyền đạt thông tin sai lệch, làm cho ai đó xấu hổ hoặc gây hấn với người khác.)
Chọn A.
Câu 3
A. Cảm xúc vận động từ hiện tại hướng tới tương lai.
B. Bài thơ là dòng hồi tưởng về quá khứ rồi lại trở về hiện tại.
C. Bài thơ là dòng hoài niệm của nhân vật tôi về hình ảnh của mẹ trong quá khứ.
D. Bài thơ có sự đan xen giữa quá khứ, hiện tại và tương lai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. Nhện có hệ thần kinh chuỗi hạch.
B. Mực có hệ thần kinh chuỗi hạch.
C. Sứa có hệ thần kinh mạng lưới.
D. Cá có hệ thần kinh mạng lưới.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Myrcene là một hydrocarbon có trong hoa bia, nó làm cho bia có hương vị và mùi thơm đặc trưng. Công thức của myrcene được cho dưới đây:
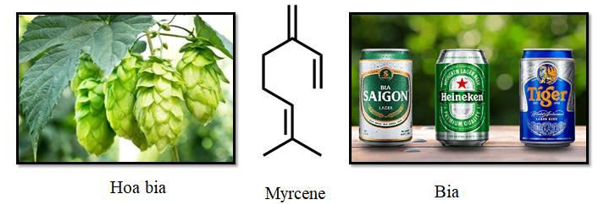
Một học sinh khi nghiên cứu về myrcene đã thu được các kết quả sau:
(a) Phần trăm khối lượng của cacbon trong myrcene bằng 88,235%.
(c) Myrcene là hydrocarbon thơm.
(d) Khung carbon của myrcene được hình thành từ 2 phân tử isoprene.
Trong các kết quả trên, kết quả đúng là
A. kết quả (a) và (b).
B. kết quả (b) và (c).
C. cả 4 kết quả.
D. kết quả (a) và (d).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Tư tưởng trong nghệ thuật là tư tưởng yên lặng.
B. Nghệ thuật luôn phải gắn với tư tưởng.
C. Phải có tư tưởng thì nghệ thuật mới có thế tồn tại được.
D. Cái yên lặng của một câu thơ lắng sâu xuống tư tưởng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Soda (\(N{a_2}C{O_3}\)) khi để lâu ngày bị chuyển hóa một phần thành \(NaHC{O_3}\)và hút ẩm tạo thành hỗn hợp X gồm \(N{a_2}C{O_3},\,NaHC{O_3}\)và \({H_2}O\). Hòa tan hoàn toàn 12,3 gam X trong nước, thu được 100 mL dung dịch Y. Tiến hành các thí nghiệm sau:
Thí nghiệm 1: Cho 25 mL dung dịch HCl 1M vào 10 mL dung dịch Y sau đó đun nhẹ. Chuẩn độ dung dịch thu được với chỉ thị phenolphthalein đến khi xuất hiện màu hồng nhạt thì thấy hết 25 mL dung dịch NaOH 0,2M.
Thí nghiệm 2: Cho 10 mL dung dịch NaOH 1M vào 10 mL Y sau đó thêm tiếp dung dịch \(BaC{l_2}\) đến dư vào, lọc bỏ kết tủa. Chuẩn độ nước lọc với chỉ thị phenolphthalein đến khi màu hồng vừa mất thì hết 40 mL dung dịch HCl 0,2M.
Thành phần % \(N{a_2}C{O_3}\) đã bị chuyển hóa thành \(NaHC{O_3}\) là
A. 5%.
B. 16%.
C. 10%
D. 8%.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập