khoahoc.vietjack.com
Kích hoạt VIP
khoahoc.vietjack.com
Kích hoạt VIP Đăng nhập
Tạo VIP
  2. Phòng luyện thi ĐGNL - ĐGTD
  3. ĐHQG Hà Nội

Câu hỏi:

14/01/2026 182 Lưu

Cho đồ thị hàm số \(y = f\left( x \right)\) như hình vẽ bên. Tìm \(m\) để phương trình \(f\left( x \right) + 1 = m\) có đúng 3 nghiệm?

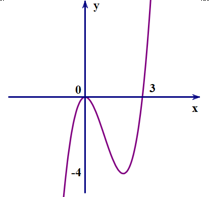
Cho đồ thị hàm số y = f(x) như hình vẽ bên. Tìm m để phương trình f(x) +m = 1 có đúng 3 nghiệm? (ảnh 1)

A. \( - 3 < m < 1\).  
B. \( - 4 < m < 0\).      
C. \( - 5 < m < 1\). 
D. \( - 4 < m < 1\).
Xem lời giải

Câu hỏi trong đề: Đề tham khảo ĐGNL ĐHQG Hà Nội (HSA) năm 2026-2027 (Đề 5) !!

Flashcard Bắt Đầu Thi Giao bài

Quảng cáo

Trả lời:

verified Giải bởi Vietjack

Ta có: \(f\left( x \right) + 1 = m \Leftrightarrow f\left( x \right) = m - 1\).

Số nghiệm của phương trình \(f\left( x \right) + 1 = m\) bằng số giao điểm của đồ thị \(y = f\left( x \right)\) và đường thẳng \(y = m - 1\).

Dựa vào đồ thị, ta có ycbt

 \( \Leftrightarrow - 4 < m - 1 < 0 \Leftrightarrow - 3 < m < 1\). Chọn A.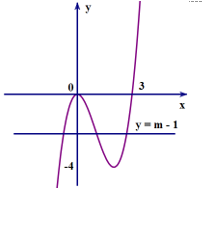
Cho đồ thị hàm số y = f(x) như hình vẽ bên. Tìm m để phương trình f(x) +m = 1 có đúng 3 nghiệm? (ảnh 2)

Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay

Các sản phẩm khác của Vietjack:
  1. Combo 3 khóa học Toán - Văn - Anh lớp 1-12 chỉ với 250k
  2. Phòng luyện 1000 đề VIP Đgnl các trường ĐHQGHN, Tp.HCM, Bách Khoa, tốt nghiệp THPT chỉ với 399k
  3. Mã giảm giá 20% sản phẩm sách VietJack trên Shopee mall
Avatar

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hàm số y=fx xác định và liên tục trên ℝ, có bảng biến thiên như sau:

loading...

Xác định số nghiệm của phương trình 2fx−23fx+1=0, biết f−4=0 (nhập đáp án vào ô trống).

 __

Lời giải

Đáp án:

1. 3

Ta có \(2\left[ {f\left( x \right)} \right]{}^2 - 3f\left( x \right) + 1 = 0 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = 1\\f\left( x \right) = \frac{1}{2}\end{array} \right.\).

• Xét phương trình \(f\left( x \right) = 1\) (1). Quan sát bảng biến thiên ta thấy đồ thị hàm số \(y = f\left( x \right)\) cắt đường thẳng \(y = 1\) tại 1 điểm duy nhất.

• Xét phương trình \(f\left( x \right) = \frac{1}{2}\) (2). Quan sát bảng biến thiên ta thấy đồ thị hàm số \(y = f\left( x \right)\) cắt đường thẳng \(y = \frac{1}{2}\) tại 2 điểm phân biệt.

Đồng thời nghiệm của phương trình (1) khác 2 nghiệm của phương trình (2) nên số nghiệm của phương trình đã cho là 3.

Đáp án cần nhập là: \(3\).

Câu 2

Cho một hộp kín có 6 thẻ ATM của BIDV và 4 thẻ ATM của Vietcombank. Lấy ngẫu nhiên lần lượt 2 thẻ (lấy không hoàn lại). Tìm xác suất để lần thứ hai lấy được thẻ ATM của Vietcombank nếu biết lần thứ nhất đã lấy được thẻ ATM của BIDV.
A. \[\frac{5}{9}\].  
B. \[\frac{2}{3}\]. 
C. \[\frac{7}{9}\].  
D. \[\frac{4}{9}\].

Lời giải

Gọi A là biến cố “lần thứ hai lấy được thẻ ATM Vietcombank”, B là biến cố “lần thứ nhất lấy được thẻ ATM của BIDV”. Ta cần tìm \[P\left( {A|B} \right)\].

Sau khi lấy lần thứ nhất (biến cố B đã xảy ra) trong hộp còn lại 9 thẻ (trong đó 4 thẻ Vietcombank) nên \[P\left( {A|B} \right) = \frac{4}{9}\]. Chọn D.

Câu 3

Hàng ngày mực nước tại một cảng biển lên xuống theo thủy triều. Độ sâu hm của mực nước theo thời gian t (giờ) trong một ngày cho bởi công thức:

h=16+7sinπ12t với 0≤t≤24.

Tìm thời điểm t (giờ) mà mực nước tại cảng là cao nhất (nhập đáp án vào ô trống).

__

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho hàm số bậc ba \[y = f\left( x \right)\]. Hàm số \(y = f'\left( x \right)\) có đồ thị như hình dưới đây.

Cho hàm số bậc ba y = f(x) Hàm số y = f'(x) có đồ thị như hình dưới đây. (ảnh 1)

Hàm số \[y = f\left( {2 - {x^2}} \right)\] đồng biến trên khoảng nào trong các khoảng dưới đây?
A. \[\left( { - \infty ; - 1} \right)\]. 
B. \(\left( { - \infty \,;\,1} \right)\).    
C. \(\left( { - 1\,;\,1} \right)\).               
D. \(\left( {4\,;\,5} \right)\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Một xạ thủ bắn lần lượt hai viên đạn vào bia. Xác suất bắn trúng đích của viên thứ nhất và viên thứ hai lần lượt là \(0,7\) và \(0,8\). Biết rằng kết quả các lần bắn độc lập với nhau. Xác suất của biến cố: “Cả hai lần bắn đều không trúng đích” là:
A. \[0,05\].    
  B. \[0,06\].   
C. \[0,08\].   
D. \[0,07\].

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho phương trình \[\left( {m - 1} \right){x^2} - 2\left( {m + 2} \right)x + m + 1 = 0\], với \(m\) là tham số. Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình có hai nghiệm phân biệt \({x_1},{x_2}\) sao cho \({x_1} + {x_2} - {x_1}{x_2}\) là một số nguyên?
A. 3.      
B. 4.   
C. 5.      
D. 6.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Trong không gian \[Oxyz\], cho điểm \(I\left( {1;0;0} \right)\)và đường thẳng \(d:\frac{{x - 1}}{1} = \frac{{y - 1}}{2} = \frac{{z + 2}}{1}\). Phương trình mặt cầu \[\left( S \right)\] có tâm I và cắt đường thẳng d tại hai điểm A, B sao cho tam giác IAB đều là:

 
A. \({\left( {x + 1} \right)^2} + {y^2} + {z^2} = \frac{{20}}{3}\).
B. \({\left( {x - 1} \right)^2} + {y^2} + {z^2} = \frac{{20}}{3}\).     
C. \({\left( {x - 1} \right)^2} + {y^2} + {z^2} = \frac{{16}}{4}\).    
D. \({\left( {x - 1} \right)^2} + {y^2} + {z^2} = \frac{5}{3}\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Đăng ký

Bạn đã có tài khoản?

Khóa học 1 - 12
THPT
THCS
Phòng luyện đề
ĐGNL - ĐGTD
Tốt nghiệp THPT
Ôn vào 10
Ôn vào 6
Tài liệu
THPT
THCS
Tin Tuyển Sinh
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack72. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập