Cho \(\Delta ABC\) vuông tại \(A\), vẽ đường tròn tâm \(O\) đường kính \(AB\), đường tròn tâm \(O\) cắt \(BC\) tại \(D\). Từ \(A\) kẻ đường thẳng vuông góc với \(OC\) tại \(H\), \(AH\) cắt \(\left( O \right)\) tại điểm thứ hai là \(E\).
a) Chứng minh \(OE \bot CE\) và 4 điểm \(A,\,C,\,E,\,O\) cùng thuộc một đường tròn.
b) Chứng minh \(C{A^2} = CH.CO\) và \(CH.CO = CD.CB\) .
c) Chứng minh \(\widehat {CHD} = \widehat {CBO}\) và \(E{H^2} = D{E^2} + D{H^2}\).
Cho \(\Delta ABC\) vuông tại \(A\), vẽ đường tròn tâm \(O\) đường kính \(AB\), đường tròn tâm \(O\) cắt \(BC\) tại \(D\). Từ \(A\) kẻ đường thẳng vuông góc với \(OC\) tại \(H\), \(AH\) cắt \(\left( O \right)\) tại điểm thứ hai là \(E\).
a) Chứng minh \(OE \bot CE\) và 4 điểm \(A,\,C,\,E,\,O\) cùng thuộc một đường tròn.
b) Chứng minh \(C{A^2} = CH.CO\) và \(CH.CO = CD.CB\) .
c) Chứng minh \(\widehat {CHD} = \widehat {CBO}\) và \(E{H^2} = D{E^2} + D{H^2}\).
Quảng cáo
Trả lời:
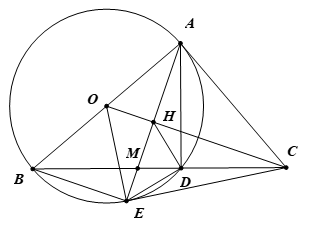
a) Chứng minh \(OE \bot CE\) và 4 điểm \(A,\,C,\,E,\,O\) cùng thuộc một đường tròn.
Xét \[\Delta AEO\] có \(OA = OE = R\), suy ra \[\Delta AEO\] cân tại \(O\)
Mà \(OH\) là đường cao ( gt)
Nên \(OH\) đồng thời là đường phân giác (tc)
Chứng minh được \[\Delta AOC = \Delta EOC\left( {cgc} \right)\]
Suy ra \[\widehat {OAC} = \widehat {OEC} = 90^\circ \]
Xét \[\Delta ACO\] có \(\widehat {OAC} = 90^\circ \)
Suy ra \(A,\,O,\,C\) cùng thuộc đường tròn đường kính \(CO\) (1)
Xét \[\Delta ECO\] có \(\widehat {CEO} = 90^\circ \)
Suy ra \(E,\,O,\,C\) cùng thuộc đường tròn đường kính \(CO\) (2)
Từ (1) và (2) suy ra \(A,\,C,\,E,\,O\) cùng thuộc đường tròn đường kính \(CO\).
b) Chứng minh \(C{A^2} = CH.CO\) và \(CH.CO = CD.CB\).
Xét \(\Delta CHA\) và \(\Delta CAO\) ta có
\(\widehat {AHC} = \widehat {OAC} = 90^\circ \)
\(\widehat {OCA}\,\)chung
Suy ra : \(\frac{{CH}}{{CA}} = \frac{{CA}}{{CO}} \Rightarrow CH.CO = C{A^2}\left( 1 \right)\)
Chứng minh tương tự ta có Suy ra : \(\frac{{CD}}{{CA}} = \frac{{CA}}{{CB}} \Rightarrow ACD.CB = C{A^2}\left( 2 \right)\)
Từ (1) và (2) suy ra \(CH.CO = CD.CB\) (đpcm)
Suy ra : \(\frac{{CH}}{{CB}} = \frac{{CD}}{{CO}}\)
c) Chứng minh \(\widehat {CHD} = \widehat {CBO}\) và \(E{H^2} = D{E^2} + D{H^2}\).
Gọi \(AE\) cắt \(BC\) tại \(M\)
Xét \(\Delta CHD\) và \(\Delta CBO\) ta có \(\frac{{CH}}{{CB}} = \frac{{CD}}{{CO}}\left( {cmt} \right)\); \(\widehat {OCB}\,\)chung
Suy ra \(\widehat {CHD} = \widehat {CBO}\left( {dpcm} \right)\) và \(\widehat {CDH}\, = \widehat {COB}\)
Suy ra \(\widehat {COA} = \widehat {HDB}\,\,\,\left( a \right)\)
Chứng minh tương tự ta có
Suy ra : \(\frac{{MB}}{{ME}} = \frac{{MA}}{{MD}}\)
Suy ra : \( \Rightarrow \widehat {MAB} = \widehat {MDE}\,\,\,\left( b \right)\)
Mặt khác: \(\widehat {OAH} + \widehat {AOH} = 90^\circ \,\,\,\left( c \right)\)
Từ (a), ( b) và (c) suy ra \(\widehat {HDM} + \widehat {MDE} = 90^\circ \) hay \(\widehat {HDE} = 90^\circ \)
Suy ra \(E{H^2} = D{E^2} + D{H^2}\).Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Chu vi hình quạt tròn bằng \(25\,{\rm{m}}\)
Nên độ dài cung tròn là: \(25 - 6 - 6 = 13\left( {\rm{m}} \right)\)
Diện tích của bồn hoa hình quạt tròn là: \({S_q} = \frac{1}{2}lR = \frac{1}{2}.13.6 = 39\left( {{{\rm{m}}^{\rm{2}}}} \right)\)
Lời giải
ĐK: \(x = - 4\);\(x \ge 4\).
\(\sqrt {x + 4} .\sqrt {x - 4} - 2\sqrt {x + 4} = 0\)
\(\sqrt {x + 4} .\left( {\sqrt {x - 4} - 2} \right) = 0\)
Suy ra \(\sqrt {x + 4} = 0\) hoặc \(\sqrt {x - 4} - 2 = 0\)
+) \(\sqrt {x + 4} = 0\)
\(x = - 4\) ( TMĐK)
+) \(\sqrt {x - 4} = 2\)
\(x - 4 = 4\)
\(x = 8\) (TMĐK)
Vậy phương trình có nghiệm \(x = - 4\) hoặc \(x = 8\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.