Giải các hệ phương trình, phương trình, bất phương trình sau

 a) \(A = 2\sqrt {27}  - 3\sqrt {12}  + \sqrt {98} \)                        b) \(\sqrt {4\left( {x - 5} \right)}  + \sqrt {9x - 45}  = \frac{{10}}{3}\)

 c) \(\frac{{\sqrt x  - 2}}{{\sqrt x  - 5}} = \frac{1}{3}\)                d) \(\frac{{5\sqrt x }}{{\sqrt x  - 2}} \ge 0\)

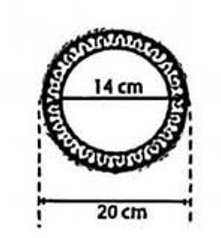
1) Bán kính đường tròn lớn là \(20:2 = 10\left( {cm} \right)\)

Bán kính đường tròn nhỏ là: \(14:2 = 7cm\)

Diện tích phần viền tráng men xanh của đĩa xứ là:

\(S = \pi \left( {{{10}^2} - {7^2}} \right) = 51\pi  \approx 51.3,14 = 160,14 \approx 160\left( {c{m^2}} \right)\)

2)

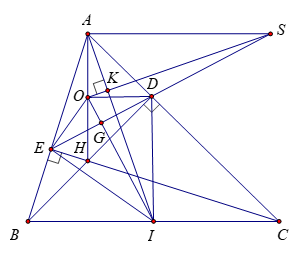
a) \(\Delta BEC\) vuông tại \(E\), có \(EI\) là đường trung tuyến ứng với cạnh huyền \(BC\), nên:

\(IE = IB = IC = \frac{1}{2}BC\)

\(\Delta BDC\) vuông tại \(D\), có \(DI\) là đường trung tuyến ứng với cạnh huyền \(BC\), nên:

\(ID = IB = IC = \frac{1}{2}BC\)

Do đó \(IB = IC = ID = IE\,\left( { = \frac{1}{2}BC} \right)\)

Vậy bốn điểm \(B\,,\,D\,,\,C\,,\,E\) cùng thuộc đường tròn tâm \(I\), đường kính \(BC\).

Xét \(\left( I \right)\), có \(DE\) là dây cung không đi qua tâm, do đó \(DE < BC\)

b) Xét \(\Delta ADB\) và \(\Delta AEC\), có: \(\widehat {ADB} = \widehat {AEC} = 90^\circ \) và \(\widehat {BAC}\) chung, nên  (g.g)

Suy ra \(\frac{{AD}}{{AE}} = \frac{{AB}}{{AC}} \Rightarrow AE.AB = AD.AC\)

\(\Delta ABC\) có hai đường cao \(BD\) và \(CE\) cắt nhau tại \(H\), nên \(H\) là trực tâm của \(\Delta ABC\)

Suy ra \(AH \bot BC\) \( \Rightarrow \widehat {ABC} + \widehat {BAH} = 90^\circ \) hay \(\widehat {IBE} + \widehat {OAE} = 90^\circ \)

Do \(IB = IE\left( { = \frac{1}{2}BC} \right)\) nên \(\Delta IBE\) cân tại \(I\) \( \Rightarrow \widehat {IEB} = \widehat {IBE}\)

\(\Delta AEH\) vuông tại \(E\), có \(EO\) là đường trung tuyến ứng với cạnh huyền \(AH\) nên \(OE = OA = OH = \frac{1}{2}AH\)

Do đó \(\Delta OAE\) cân tại \(O\) \( \Rightarrow \widehat {OEA} = \widehat {OAE}\)

Suy ra \(\widehat {IEB} + \widehat {OEA} = \widehat {IBE} + \widehat {OAE} = 90^\circ \) \( \Rightarrow \widehat {OEI} = 90^\circ \)

Vậy \(OE \bot EI\)

c) Chứng minh tương tự câu b, ta cũng có: \(OD \bot DI\)

\(\Delta ADH\) vuông tại \(D\), có \(DO\) là đường trung tuyến ứng với cạnh huyền nên: \(OD = OA = OH = \frac{1}{2}AH\)

Suy ra \(OD = OE\left( { = \frac{1}{2}AH} \right)\) nên \(O\) thuộc đường trung trực của \(DE\)

Mà \(ID = IE\left( { = \frac{1}{2}BC} \right)\) nên \(I\) thuộc đường trung trực của \(DE\)

Do đó \(OI\) là đường trung trực của \(DE\) hay \(OI \bot DE\)

Gọi \(G\) là giao điểm của \(OI\) và \(DE\); \(K\) là giao điểm của \(AI\) và \(OS\).

Ta có:  (g.g) \( \Rightarrow \frac{{OD}}{{OI}} = \frac{{OG}}{{OD}} \Rightarrow O{D^2} = OG.OI\)

 (g.g) \( \Rightarrow \frac{{OK}}{{OG}} = \frac{{OI}}{{OS}} \Rightarrow OK.OS = OG.OI\)

Do đó \(OK.OS = O{D^2} = O{A^2}\)\( \Rightarrow \frac{{OK}}{{OA}} = \frac{{OA}}{{OS}}\)

Xét \(\Delta OKA\) và \(\Delta OAS\), có: \(\frac{{OK}}{{OA}} = \frac{{OA}}{{OS}}\) và \(\widehat {AOS}\) chung

Do đó  (c.g.c)

\( \Rightarrow \widehat {OAS} = \widehat {OKA} = 90^\circ \) \( \Rightarrow SA \bot AO\) hay \(SA \bot AH\), mà \(AH \bot BC\) nên \(SA\,{\rm{//}}\,BC\) (đpcm)

1) Gọi chiều dài và chiều rộng ban đầu của khu vườn lần lượt là: \[x,{\rm{ }}y{\rm{ }}\left( m \right){\rm{ }}\left( {x,{\rm{ }}y > 1} \right).\]

Diện tích ban đầu của khu vườn là: \[xy{\rm{ }}\left( {{m^2}} \right)\]

Vì chiều dài của khu vườn sau khi tăng thêm 3m là \(x + 3\) (m) và chiều rộng của khu vườn sau

khi tăng thêm 2m là \(y + 2\) (m) thì diện tích khu vườn tăng 84m2 nên ta có phương trình: \(\left( {x + 3} \right)\left( {y + 2} \right) = xy + 84\) hay \(2x + 3y = 78\) (1)

Vì chiều dài, chiều rộng của khu vườn lúc sau khi đều giảm đi 1m lần lượt là \(x - 1\)(m), \(y - 1\)(m) 

thì diện tích khu vườn giảm đi 31m2 nên ta có phương trình:

\(\left( {x - 1} \right)\left( {y - 1} \right) = xy - 31\) hay \(x + y = 32\) (2)

Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}2x + 3y = 78\\x + y = 32\end{array} \right.\)       suy ra \(\left\{ \begin{array}{l}x = 18(tm)\\y = 14(tm)\end{array} \right.\).

Vậy chiều dài và chiều rộng ban đầu của khu vườn lần lượt là 18m, 14m.

2) Gọi số xe ban đầu đội vận chuyển đã chuẩn bị là: x (xe) (\[x \in {\mathbb{N}^*}\]).

Số tấn hàng trên mỗi xe theo như dự định của đội là: \(\frac{{36}}{x}\) (tấn/xe).

Trong thực tế số chiếc xe vận chuyển hàng của đội là: \(x + 3\) (xe).

Số tấn hàng trên mỗi xe trong thực tế của đội là: \(\frac{{36}}{{x + 3}}\) (tấn/xe).

Vì lượng hàng phải chở trên mỗi xe trong thực tế giảm xuống 1 tấn so với kế hoạch ban đầu nên

ta có phương trình: \(\frac{{36}}{x} - 1 = \frac{{36}}{{x + 3}}\) suy ra \[x =  - 12\] (ktm) hoặc \[x = 9\] (tm).

Vậy ban đầu đội vận chuyển đã chuẩn bị 9 xe.