Phân thức nghịch đảo của phân thức \( - \frac{{3{y^2}}}{{2x}}\) là
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án đúng là: C
Phân thức nghịch đảo của phân thức \( - \frac{{3{y^2}}}{{2x}}\) là \( - \frac{{2x}}{{3{y^2}}}.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
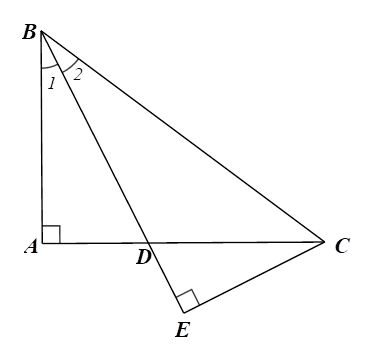
a) Xét \(\Delta ABC\) vuông tại theo định lí Pytagore ta có: \(B{C^2} = A{B^2} + A{C^2} = {8^2} + {6^2} = 64 + 36 = 100\) \(A,\)
Suy ra \(BC = \sqrt {100} = 10{\rm{\;cm}}.\)
Vì \(BD\) là tia phân giác của góc \(ABC\) nên suy ra:
\[\frac{{DA}}{{DC}} = \frac{{BA}}{{BC}} = \frac{6}{{10}} = \frac{3}{5}.\]
b) Theo đề bài, \(CE \bot BD\) tại \(E\) nên \(\widehat {BEC} = 90^\circ .\)
Xét \(\Delta ABD\) và \(\Delta EBC\) có:
\(\widehat {BAD} = \widehat {BEC} = 90^\circ \) và \(\widehat {{B_1}} = \widehat {{B_2}}\) (vì \(BD\) là tia phân giác của góc \(ABC)\)
Do đó (g.g).
Suy ra: \(\frac{{BD}}{{AD}} = \frac{{BC}}{{EC}}\) (tỉ số cạnh tương ứng).
Do đó \(BD \cdot EC = AD \cdot BC.\)
c) Từ \(\frac{{DA}}{{DC}} = \frac{{AB}}{{BC}}\) suy ra \(\frac{{CD}}{{BC}} = \frac{{AD}}{{AB}}\)\(\left( 1 \right)\)
Vì (câu b) nên \(\frac{{AD}}{{EC}} = \frac{{AB}}{{EB}},\) suy ra \(\frac{{AD}}{{AB}} = \frac{{EC}}{{EB}}\)\(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra: \(\frac{{CD}}{{BC}} = \frac{{CE}}{{BE}}.\)
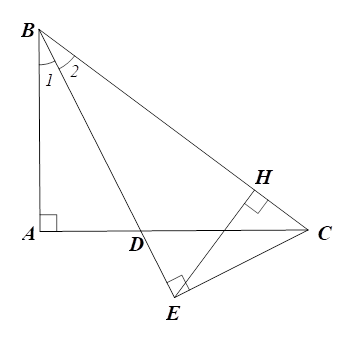
d) Tương tự câu b ta chứng minh được:
⦁ (g.g) nên \(\frac{{CH}}{{CE}} = \frac{{CE}}{{CB}}.\)
Suy ra \(CH \cdot CB = C{E^2}\,\,\left( 3 \right)\)
⦁ (g.g) nên
Suy ra \(ED \cdot EB = C{E^2}\left( 4 \right)\)
Từ \(\left( 3 \right)\) và \(\left( 4 \right)\) suy ra: \(CH \cdot HB = ED \cdot EB.\)
Lời giải
Hướng dẫn giải
a) Ta có \(9 - {x^2} = \left( {3 - x} \right)\left( {3 + x} \right).\)
\[2 - \frac{{x + 5}}{{3 + x}} = \frac{{2\left( {3 + x} \right) - \left( {x + 5} \right)}}{{3 + x}} = \frac{{6 + 2x - x - 5}}{{3 + x}} = \frac{{x + 1}}{{x + 3}}.\]
Điều kiện xác định của biểu thức \(A\) là \(\left\{ \begin{array}{l}x + 3 \ne 0\\x - 3 \ne 0\\9 - {x^2} \ne 0\\2 - \frac{{x + 5}}{{3 + x}} \ne 0\end{array} \right.\) hay \(\left\{ \begin{array}{l}x + 3 \ne 0\\x - 3 \ne 0\\x + 1 \ne 0\end{array} \right.,\) tức là \(\left\{ \begin{array}{l}x \ne - 3\\x \ne 3\\x \ne - 1\end{array} \right..\)
Vậy điều kiện xác định của biểu thức \(A\) là \(x \ne - 3,\,\,x \ne 3\) và \(x \ne - 1.\)
b) Với \(x \ne - 3,\,\,x \ne 3\) và \(x \ne - 1\) ta có:
\(A = \left( {\frac{x}{{x + 3}} - \frac{2}{{x - 3}} + \frac{{{x^2} - 1}}{{9 - {x^2}}}} \right):\left( {2 - \frac{{x + 5}}{{3 + x}}} \right)\)
\( = \left[ {\frac{x}{{x + 3}} - \frac{2}{{x - 3}} - \frac{{{x^2} - 1}}{{\left( {x - 3} \right)\left( {x + 3} \right)}}} \right]:\frac{{x + 1}}{{x + 3}}\)
\( = \frac{{x\left( {x - 3} \right) - 2\left( {x + 3} \right) - \left( {{x^2} - 1} \right)}}{{\left( {x - 3} \right)\left( {x + 3} \right)}}:\frac{{x + 1}}{{x + 3}}\)
\( = \frac{{{x^2} - 3x - 2x - 6 - {x^2} + 1}}{{\left( {x - 3} \right)\left( {x + 3} \right)}}.\frac{{x + 3}}{{x + 1}}\)
\[ = \frac{{ - 5x - 5}}{{\left( {x - 3} \right)\left( {x + 3} \right)}}.\frac{{x + 3}}{{x + 1}}\]\[ = \frac{{ - 5\left( {x + 1} \right)}}{{\left( {x - 3} \right)\left( {x + 1} \right)}} = \frac{{ - 5}}{{x - 3}}.\]
Vậy với \(x \ne - 3,\,\,x \ne 3\) và \(x \ne - 1\) thì \(A = \frac{{ - 5}}{{x - 3}}.\)
c) Với \({x^2} - x - 2 = 0\) ta có \({x^2} - 2x + x - 2 = 0\)
\(x\left( {x - 2} \right) + \left( {x - 2} \right) = 0\)
\(\left( {x - 2} \right)\left( {x + 1} \right) = 0\)
Suy ra \(x - 2 = 0\) hoặc \(x + 1 = 0\)
\(x = 2\) (thỏa mãn điều kiện) hoặc \(x = - 1\) (không thỏa mãn điều kiện)
Thay \(x = 2\) vào biểu thức \(A = \frac{{ - 5}}{{x - 3}}\) ta được: \(A = \frac{{ - 5}}{{2 - 3}} = \frac{{ - 5}}{{ - 1}} = 5.\)
Vậy nếu \({x^2} - x - 2 = 0\) thì \(A = 5.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.