Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(B,{\rm{ }}AB = 3a,{\rm{ }}BC = 4a.\) Cạnh bên \(SA\) vuông góc với đáy. Góc tạo bởi giữa \(SC\) và đáy bằng \(60^\circ \). Gọi là trung điểm của \(AC\), khoảng cách giữa hai đường thẳng \(AB\) và \(SM\) bằng:
A. \(a\sqrt 3 \).
B. \(\frac{{10a\sqrt 3 }}{{\sqrt {79} }}\).
C. \(\frac{{5a}}{2}\).
D. \(5a\sqrt 3 \).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Sử dụng định lí Pythagore ta tính được \(AC = 5a\).
Có \(\left( {SC,\left( {ABC} \right)} \right) = \widehat {SCA} = 60^\circ \). Suy ra \(SA = AC \cdot \tan 60^\circ = 5a\sqrt 3 \).
Gọi \(N\) là trung điểm \(BC\)\( \Rightarrow AB{\rm{//}}\left( {SMN} \right)\)
\( \Rightarrow d\left( {AB,{\rm{ }}SM} \right) = d\left( {A,\left( {SMN} \right)} \right)\).
Dựng \(AH \bot MN\) tại \(H\) trong mặt phẳng \(\left( {ABC} \right)\).
Dựng \(AK \bot SH\) tại \(K\) trong mặt phẳng \(\left( {{\rm{S}}AH} \right)\).
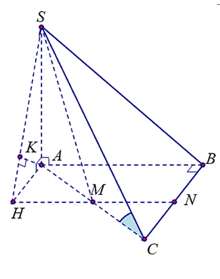
\( \Rightarrow AK \bot \left( {SMN} \right)\) tại \(K\) nên \(d\left( {A,\left( {SMN} \right)} \right) = AK\)\[ \Rightarrow d\left( {AB,SM} \right) = AK\].
Ta có: \(AH = NB = 2a\).
Khi đó, \(\frac{1}{{A{K^2}}} = \frac{1}{{A{H^2}}} + \frac{1}{{S{A^2}}} = \frac{1}{{4{a^2}}} + \frac{1}{{75{a^2}}} = \frac{{79}}{{300{a^2}}}\) \( \Rightarrow AK = \frac{{10a\sqrt 3 }}{{\sqrt {79} }}\). Chọn B.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Xuất khẩu và nhập khẩu đều tăng trong giai đoạn 2000 - 2020. → Chọn B.
Câu 2
A. \(m < \frac{{ - 2}}{5}\).
A. \(m < \frac{{ - 2}}{5}\).
C. \(m \ge \frac{{ - 2}}{5}\).
D. \(m \le \frac{{ - 2}}{5}\).
Lời giải
Tam thức bậc hai \(f\left( x \right) = {x^2} + 2mx + m - 2\) có:
\(\Delta ' = {m^2} - m + 2 = {\left( {m - \frac{1}{2}} \right)^2} + \frac{7}{4} \ge \frac{7}{4} > 0\) với mọi \(m \in \mathbb{R}\).
Do đó \(f\left( x \right)\) có hai nghiệm phân biệt \({x_1},{x_2}\left( {{x_1} < {x_2}} \right)\) với mọi \(m \in \mathbb{R}\).
Để \(f\left( x \right) < 0\) với mọi \(x \in \left( {1;\,\,2} \right)\) thì \({x_1} \le 1 < 2 \le {x_2}\)
\[ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{f\left( 1 \right) \le 0}\\{f\left( 2 \right) \le 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{1 + 2m + m - 2 \le 0}\\{4 + 4m + m - 2 \le 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{3m - 1 \le 0}\\{5m + 2 \le 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{m \le \frac{1}{3}}\\{m \le \frac{{ - 2}}{5}}\end{array}} \right. \Leftrightarrow m \le \frac{{ - 2}}{5}\].
Vậy \(m \le \frac{{ - 2}}{5}\) thì \({x^2} + 2mx + m - 2 < 0\) với mọi \(x \in \left( {1;\,\,2} \right)\). Chọn D.
Câu 3
A. \(\frac{{a\sqrt {21} }}{{14}}\).
B. \(\frac{{a\sqrt {21} }}{7}\).
C. \(\frac{{a\sqrt 3 }}{{14}}\).
D. \(\frac{{a\sqrt 3 }}{7}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. Được ưu tiên đầu tư, có khả năng phát triển các ngành mới và lan tỏa đến lãnh thổ khác.
B. Phạm vi vùng luôn cố định, ranh giới không có sự thay đổi theo thời gian.
C. Đóng góp lớn vào tốc độ tăng trưởng quy mô GDP cả nước.
D. Cơ sở vật chất phát triển, có tiềm lực kinh tế lớn và giữ vai trò động lực.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. The belief that both joy and sorrow are necessary in life.
B. The idea that joy is the only thing worth pursuing.
C. The experience of joy and sorrow in our lives.
D. The question of why we need both joy and sorrow.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. 500-year-old rock art.
B. northern New South Wales.
C. granite rock.
D. intense and rapid temperature change of the fires.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(\frac{{35}}{{132}}\).
B. \(\frac{{35}}{{144}}\).
C. \[\frac{2}{{11}}\].
D. \[\frac{{35}}{{66}}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập