Tại một cuộc thi có 300 thí sinh. Biết rằng, hai thí sinh bất kì hoặc quen nhau hoặc không quen nhau, và không có ba thí sinh nào đôi một quen nhau. Xác định giá trị lớn nhất của n (nhập đáp án vào ô trống) sao cho các điều kiện sau đây thỏa mãn:

• Mỗi thí sinh quen tối đa n thí sinh khác và có ít nhất một thí sinh quen đúng n thí sinh khác.

• Với mọi số nguyên dương m mà 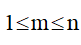, tồn tại ít nhất 1 thí sinh quen đúng m thí sinh khác.

Đáp án  ____

Trước hết ta chứng minh \[n \le 200\]. Giả sử \[n > 200\] thỏa mãn các điều kiện của đề bài. Khi đó mỗi thí sinh \[X\] quen biết với \[201\] thí sinh khác. Gọi \[S\] là tập hợp \[201\] thí sinh này. Theo giả thiết thì tồn tại các thí sinh quen đúng \[1,2,...,200\] thí sinh khác.

Ta nói một thí sinh có bậc \[m\] nếu người ấy quen đúng \[m\] thí sinh khác. Ta có \[X\] quen với tất cả thí sinh trong tập \[S\]. Mà trong \[3\] người luôn tồn tại ít nhất \[2\] người không quen nhau, nên \[2\] thí sinh bất kỳ trong tập \[S\] đều không quen nhau. Do đó mỗi phần tử của \[S\] có bậc tối đa là \[300 - 201 = 99\].

Từ đó suy ra mỗi phần tử trong tập \[S\] xác định tối đa \[99\] bậc phân biệt (từ \[1\] đến \[99\]). Mặt khác, có \[99\] người khác ngoài \[S\] cho nên tổng số bậc tối đa của \[300\] thí sinh là \[99 + 99 = 198 < 201\] (mâu thuẫn). Vậy \[n \le 200\].

Bây giờ ta sẽ đi xây dựng một trường hợp thỏa mãn \[n = 200\]. Thật vậy, kí hiệu \[{A_1},{A_2},...,{A_{100}}\] là \[100\] thí sinh loại \[A\], kí hiệu \[{B_1},{B_2},...,{B_{200}}\] là \[200\] thí sinh còn lại và gọi họ là các thí sinh loại \[B\]. Giả sử rằng:

(1) Với mỗi \[i \in \left\{ {1;2;...;100} \right\}\], \[{A_i}\] quen biết với \[B_j^{}\] khi và chỉ khi \[j \ge i\].

(2) Hai thí sinh cùng loại bất kỳ đều không quen nhau.                        

• Từ điều kiện (2) thì cứ \[3\] thí sinh bất kỳ, có ít nhất \[2\] em không quen nhau.

• Từ (1) thì mỗi thí sinh \[{A_i}\] quen đúng với đúng \[201 - i\] thí sinh khác. Do đó có những thí sinh quen đúng \[200,199,...,101\] thí sinh khác.

• Từ điều kiện (1) thì với mỗi \[j \in \left\{ {1;2;...;100} \right\}\], \[{B_j}\] quen đúng với \[j\] thí sinh khác, tức là có những thí sinh quen với đúng \[1;2;...;100\] thí sinh khác.

• Theo lập luận trên thí mỗi thí sinh quen với tối đa \[200\] thí sinh khác.

Vậy \[n = 200\] là giá trị lớn nhất thỏa mãn đề bài.