PHẦN II. TỰ LUẬN

Cho biểu thức \[A = \frac{{{x^3} - 1}}{{{x^2} - 4}} \cdot \left( {\frac{1}{{x - 1}} - \frac{{x + 1}}{{{x^2} + x + 1}}} \right).\]

a) Viết điều kiện xác định của biểu thức \(A.\)

b) Rút gọn biểu thức \(A.\)

c) Tính giá trị của biểu thức \(A\) biết \(\left| {x + 3} \right| = 1.\)

Hướng dẫn giải

Điều kiện \(a,\,\,b,\,\,c \ne 0.\)

Với \[a + b + c = 0,\] ta có \(a + b =  - c;\,\,b + c =  - a;\,\,c + a =  - b.\)

Ta có \(C = \left( {\frac{{a - b}}{c} + \frac{{b - c}}{a} + \frac{{c - a}}{b}} \right)\left( {\frac{c}{{a - b}} + \frac{a}{{b - c}} + \frac{b}{{c - a}}} \right)\)

\( = \underbrace {\left( {\frac{{a - b}}{c} + \frac{{b - c}}{a} + \frac{{c - a}}{b}} \right) \cdot \frac{c}{{a - b}}}_M + \underbrace {\left( {\frac{{a - b}}{c} + \frac{{b - c}}{a} + \frac{{c - a}}{b}} \right) \cdot \frac{a}{{b - c}}}_N + \underbrace {\left( {\frac{{a - b}}{c} + \frac{{b - c}}{a} + \frac{{c - a}}{b}} \right) \cdot \frac{b}{{c - a}}}_P\)

Xét \(M = \left( {\frac{{a - b}}{c} + \frac{{b - c}}{a} + \frac{{c - a}}{b}} \right) \cdot \frac{c}{{a - b}}\)

\( = 1 + \frac{c}{{a - b}} \cdot \left( {\frac{{b - c}}{a} + \frac{{c - a}}{b}} \right)\)\( = 1 + \frac{c}{{a - b}} \cdot \frac{{{b^2} - bc + ac - {a^2}}}{{ab}}\)

\( = 1 + \frac{c}{{a - b}} \cdot \frac{{\left( {b - a} \right)\left( {b + a} \right) - c\left( {b - a} \right)}}{{ab}}\)\( = 1 + \frac{c}{{a - b}} \cdot \frac{{\left( {b - a} \right)\left( {b + a - c} \right)}}{{ab}}\)

\[ = 1 + \frac{c}{{a - b}} \cdot \frac{{ - \left( {a - b} \right)\left( { - c - c} \right)}}{{ab}}\]\[ = 1 + \frac{{c \cdot 2c}}{{ab}} = 1 + \frac{{2{c^3}}}{{abc}}.\]

Tương tự, \(N = 1 + \frac{{2{a^3}}}{{abc}};\,\,P = 1 + \frac{{2{b^3}}}{{abc}}.\)

Khi đó \(C = M + N + P = 1 + \frac{{2{c^3}}}{{abc}} + 1 + \frac{{2{a^3}}}{{abc}} + 1 + \frac{{2{b^3}}}{{abc}} = 3 + \frac{{2\left( {{a^3} + {b^3} + {c^3}} \right)}}{{abc}}.\)

Mặt khác, do \[a + b + c = 0\] nên ta có \[{\left( {a + b + c} \right)^3} = 0\]

Suy ra \[{\left( {a + b} \right)^3} + {c^3} + 3\left( {a + b} \right)c\left( {a + b + c} \right) = 0\]

\[{a^3} + {b^3} + 3ab\left( {a + b} \right) + {c^3} + 3\left( {a + b} \right)c\left( {a + b + c} \right) = 0\]

\[{a^3} + {b^3} + {c^3} + 3\left( {a + b} \right)\left( {ab + ac + bc + {c^2}} \right) = 0\]

\[{a^3} + {b^3} + {c^3} + 3\left( {a + b} \right)\left[ {a\left( {b + c} \right) + c\left( {b + c} \right)} \right] = 0\]

\[{a^3} + {b^3} + {c^3} + 3\left( {a + b} \right)\left( {b + c} \right)\left( {a + c} \right) = 0\]

\[{a^3} + {b^3} + {c^3} + 3\left( { - c} \right)\left( { - a} \right)\left( { - b} \right) = 0\]

\[{a^3} + {b^3} + {c^3} - 3abc = 0\]

\[{a^3} + {b^3} + {c^3} = 3abc.\]

Vậy \(C = 3 + \frac{{2 \cdot \left( {3abc} \right)}}{{abc}} = 3 + 6 = 9.\)

Hướng dẫn giải

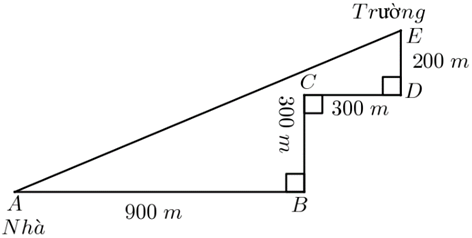
1)

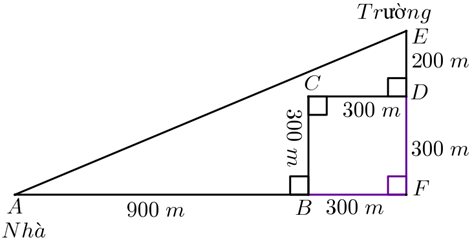
Gọi \(F\) là giao điểm của \(AB\) và \(ED.\)

Quan sát đường đi của bạn An theo hình vẽ thì đó là tứ giác \(BCDF,\) tứ giác này có \(\widehat {B\,} = \widehat {C\,} = \widehat {D\,} = 90^\circ \) nên là hình chữ nhật.

Mà \(CD = CB = 300\) m nên hình chữ nhật \(BCDF\) là hình vuông.

Do đó \(BC = CD = DF = FB = 300\) (m) và \(\widehat {BFD} = 90^\circ .\)

Ta có \(AF = AB + BF = 900 + 300 = 1\,\,200\) (m); \(EF = FD + DE = 300 + 200 = 500\) (m).

Áp dụng định lí Pythagore cho \(\Delta AEF\) vuông tại \(F\) ta có:

\(A{E^2} = A{F^2} + E{F^2}\)\( = 1\,\,{200^2} + {500^2} = 1{\rm{ }}690{\rm{ }}000.\)

Suy ra \(AE = \sqrt {1{\rm{ }}690{\rm{ }}000}  = 1\,\,300\) (m) \( = 1,3\) (km).

Thời gian đi hết quãng đường \(AE\) là: \(\frac{{1,3}}{{13}} = 0,1\) (giờ) \( = 6\) (phút).

Vậy bạn An đi từ nhà đến trường (bằng xe đạp điện) là lúc \(7\) giờ \(6\) phút.

2)

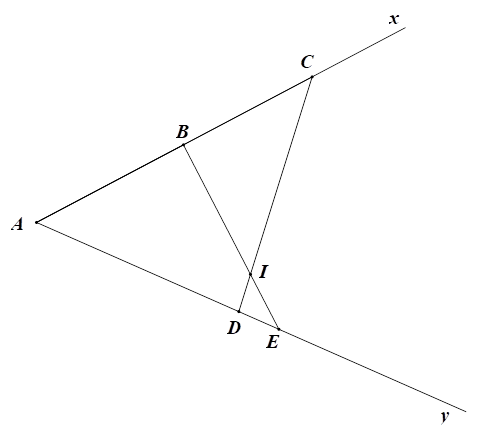
a) Xét \(\Delta ABE\) và \(\Delta ADC\) có:

\(\widehat {BAE}\) là góc chung;

\[\frac{{AB}}{{AD}} = \frac{{AE}}{{AC}}\,\,\left( {\frac{8}{{10}} = \frac{{12}}{{15}} = \frac{4}{5}} \right).\]

Do đó $\Delta ABE\backsim \Delta ADC$ (c.g.c).

b) Vì $\Delta ABE\backsim \Delta ADC$ (câu a) nên \(\frac{{AB}}{{AD}} = \frac{{BE}}{{DC}}\)

Suy ra \(AB \cdot DC = AD \cdot BE.\)

Do đó \(DC = \frac{{AD \cdot BE}}{{AB}} = \frac{{10 \cdot 10}}{8} = 12,5{\rm{\;cm}}.\)

c) Vì $\Delta ABE\backsim \Delta ADC$ (câu a) nên $\widehat{AEB}=\widehat{ACD}$ (hai góc tương ứng).

Xét \(\Delta CBI\)  và \(\Delta EDI\) có:

\(\widehat {BCI} = \widehat {DEI}\) (do \(\widehat {AEB} = \widehat {ACD})\) và \(\widehat {BIC} = \widehat {DIE}\) (hai góc đối đỉnh)

Do đó $\Delta CBI\backsim \Delta EDI$ (g.g).

Suy ra \(\frac{{IC}}{{IE}} = \frac{{IB}}{{ID}}\) (tỉ số cạnh tương ứng) nên \[IB \cdot IE = ID \cdot IC.\]