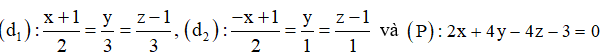Một viên gạch hình vuông có cạnh thay đổi được đặt nội tiếp trong một hình vuông có cạnh bằng \(20\,{\rm{cm}}\), tạo thành bốn tam giác xung quanh như hình vẽ. Tìm tất cả các giá trị của \[x\] để diện tích viên gạch không vượt quá \(232\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
D. \[14 \le x \le 16\].
Quảng cáo
Trả lời:
Gọi \[E,\,F\,,\,G\,,\,H\] là bốn đỉnh của viên gạch hình vuông nội tiếp trong hình vuông \[ABCD\] có cạnh \(20\,{\rm{cm}}\) như hình vẽ dưới đây.
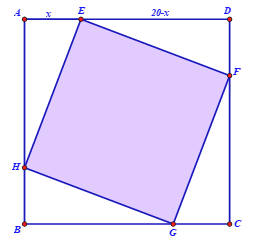
Ta có cạnh viên gạch là \[EF = \sqrt {{x^2} + {{\left( {20 - x} \right)}^2}} = \sqrt {2{x^2} - 40x + 400} \].
Diện tích của viên gạch là: \[E{F^2} = 2{x^2} - 40x + 400\].
Theo đề ta có diện tích viên gạch không vượt quá \(232\,c{m^2}\) .
Tức là \[2{x^2} - 40x + 400 \le 232 \Leftrightarrow 2{x^2} - 40x + 168 \le 0 \Leftrightarrow 6 \le x \le 14\]. Chọn B.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Nếu gửi ở ngân hàng có lãi suất \(6\% /\)năm thì sau 2 năm số tiền cả vốn lẫn lãi thu được là: \(50{\left( {1 + \frac{6}{{100}}} \right)^2} = 56,18\) (triệu đồng).
Đáp án cần nhập là: 56,18.
Câu 2
Lời giải
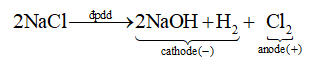
Chọn A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.