Cho hàm số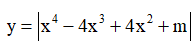 
với là tham số. Tổng tất cả các giá trị của tham số để 
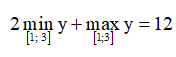bằng (nhập đáp án vào ô trống).
Đáp án ___
Quảng cáo
Trả lời:
Giải bởi Vietjack
Xét hàm số \(f\left( x \right) = {x^4} - 4{x^3} + 4{x^2} + m\) trên \(\left[ {1\,;\,\,3} \right] \Rightarrow \left\{ {\begin{array}{*{20}{l}}{\mathop {\min }\limits_{\left[ {1\,;\,\,3} \right]} f(x) = m}\\{\mathop {\max }\limits_{_{\left[ {1\,;\,\,3} \right]}} f(x) = m + 9}\end{array}} \right..\)
• TH1: Với \(m > 0\) suy ra \(\left\{ {\begin{array}{*{20}{l}}{{y_{\min }} = m}\\{{y_{\max }} = m + 9}\end{array}} \right.\).
Do đó \(2{y_{\min }} + {y_{\max }} = 2m + m + 9 = 12 \Leftrightarrow m = 1\) (thoả mãn).
• TH2: Với \(m + 9 < 0 \Leftrightarrow m < - 9\) suy ra \(\left\{ {\begin{array}{*{20}{l}}{{y_{\min }} = \left| {m + 9} \right|}\\{{y_{\max }} = \left| m \right|}\end{array}} \right.\).
Do đó \(2{y_{\min }} + {y_{\max }} = 2\left| {m + 9} \right| + \left| m \right| = 12 \Leftrightarrow 2\left( { - m - 9} \right) - m = 12 \Leftrightarrow m = - 10\) (thoả mãn).
• TH3: Với \( - 9 < m < 0\) suy ra \[\left\{ {\begin{array}{*{20}{l}}{{y_{\min }} = 0}\\{{y_{\max }} = \left\{ {\left| m \right|;\,\,\left| {m + 9} \right|} \right\}}\end{array}} \right.\].
Do đó \(2{y_{\min }} + {y_{\max }} = 12 \Leftrightarrow {y_{\max }} = 12 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\left| m \right| = 12}\\{\left| {m + 9} \right| = 12}\end{array}} \right.\) (không thoả mãn).
Nên \(m \in \left\{ { - 10\,;\,\,1} \right\}\). Do đó, tổng các giá trị của \[m\] là \( - 10 + 1 = - 9\).
Đáp án cần nhập là: −9.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. Biểu cảm.
B. Tự sự.
C. Miêu tả.
D. Nghị luận.
Lời giải
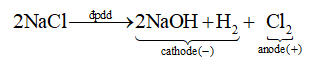
Phương thức biểu đạt chính của đoạn thơ là biểu cảm. Chọn A.
Lời giải
Đối tượng chính được đề cập đến trong đoạn trích là nhà văn Bảo Ninh. Chọn A.
Câu 3
A. Biểu cảm.
B. Miêu tả.
C. Tự sự.
D. Nghị luận.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. Vai trò của thiên nhiên đối với việc học tập và phát triển của trẻ em.
B. Nguồn gốc của loài người xuất phát từ tự nhiên.
C. Phương pháp giúp trẻ kết nối và hòa nhập với thiên nhiên.
D. Con người cần tìm cách thích nghi với thiên nhiên.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. 42,3 m.
B. 42,5 m
C. 42 m.
D. 41 m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \[8 \le x \le 12\].
B. \[6 \le x \le 14\].
C. \[12 \le x \le 14\].
D. \[14 \le x \le 16\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập