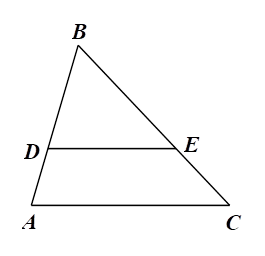PHẦN I. TRẮC NGHIỆM KHÁCH QUAN
Một trường THCS phát động phong trào biểu diễn văn nghệ nhân ngày nhà giáo Việt Nam 20/11 cho học sinh tất cả các lớp. Biết rằng mỗi lớp chỉ biểu diễn tối đa 3 tiết mục. Bảng thống kê số tiết mục đăng kí tham gia diễn văn nghệ của từng lớp như bảng dưới đây:
Lớp
6A
6B
7A
7B
8A
8B
9A
9B
Số tiết mục
2
3
5
3
2
2
3
2
Theo em, số liệu của lớp nào trong bản trên là không hợp lí?
Một trường THCS phát động phong trào biểu diễn văn nghệ nhân ngày nhà giáo Việt Nam 20/11 cho học sinh tất cả các lớp. Biết rằng mỗi lớp chỉ biểu diễn tối đa 3 tiết mục. Bảng thống kê số tiết mục đăng kí tham gia diễn văn nghệ của từng lớp như bảng dưới đây:
|
Lớp |
6A |
6B |
7A |
7B |
8A |
8B |
9A |
9B |
|
Số tiết mục |
2 |
3 |
5 |
3 |
2 |
2 |
3 |
2 |
Theo em, số liệu của lớp nào trong bản trên là không hợp lí?
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 2 Toán 8 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án đúng là: B
Do mỗi lớp chỉ biểu diễn tối đa 3 tiết mục, mà theo bảng dữ liệu, số tiết mục lớp 7A biểu diễn là \(5 > 3\) nên đây là dữ liệu không hợp lí.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
1)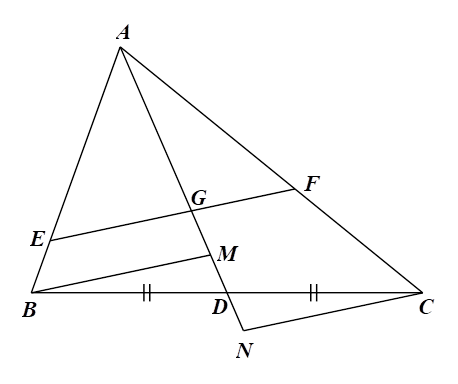
a) Xét \(\Delta ABM\) có \(EG\,{\rm{//}}\,BM,\) theo định lí Thalès ta có: \(\frac{{BE}}{{AE}} = \frac{{MG}}{{AG}}.\)
b) Xét \(\Delta DCN\) có \(BM\,{\rm{//}}\,CN,\) theo định lí Thalès ta có: \(\frac{{DN}}{{MD}} = \frac{{DC}}{{DB}}.\)
Mà \(D\) là trung điểm của \(BC\) (do \(AD\) là trung tuyến của tam giác) nên \(DC = DB.\)
Do đó \(\frac{{DN}}{{MD}} = \frac{{DC}}{{DB}} = 1,\) nên \(DM = DN.\)Suy ra \(GM + GN = GM + GM + MN = 2GM + 2MD = 2GD.\)
Lại có \(G\) là trọng tâm \(\Delta ABC\) nên \(AG = 2GD.\)
Xét \(\Delta ACN\) có \(FG\,{\rm{//}}\,CN,\) theo định lí Thalès ta có: \(\frac{{CF}}{{AF}} = \frac{{GN}}{{AG}}.\)
Suy ra \(\frac{{BE}}{{AE}} + \frac{{CF}}{{AF}} = \frac{{MG}}{{AG}} + \frac{{GN}}{{AG}} = \frac{{GM + GN}}{{AG}} = \frac{{2GD}}{{2GD}} = 1.\)
c) Xét \(\Delta ABM\) có \(EG\,{\rm{//}}\,BM,\) theo định lí Thalès ta có: \(\frac{{AB}}{{AE}} = \frac{{AM}}{{AG}}.\)
Xét \(\Delta ACN\) có \[FG\,{\rm{//}}\,CN,\] theo định lí Thalès ta có: \(\frac{{AC}}{{AF}} = \frac{{AN}}{{AG}}.\)
Suy ra \(\frac{{AB}}{{AE}} + \frac{{AC}}{{AF}} = \frac{{AM}}{{AG}} + \frac{{AN}}{{AG}}\)\( = \frac{{AG + GM + AG + GM + MN}}{{AG}}\)
\( = \frac{{2AG + 2GM + 2MD}}{{AG}}\)\( = \frac{{2AG + 2\left( {GM + MD} \right)}}{{AG}} = \frac{{2AG + 2GD}}{{AG}}\)
\( = \frac{{2AG + 2 \cdot \frac{1}{2}AG}}{{AG}} = \frac{{3AG}}{{AG}} = 3.\)
Vậy \(\frac{{AB}}{{AE}} + \frac{{AC}}{{AF}} = 3.\)
2)
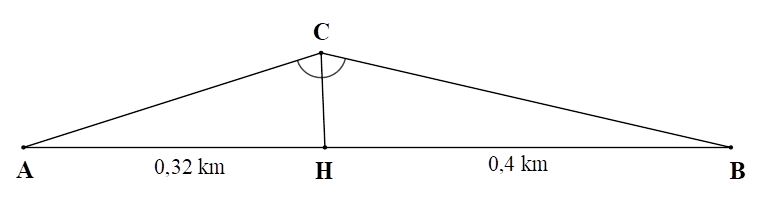
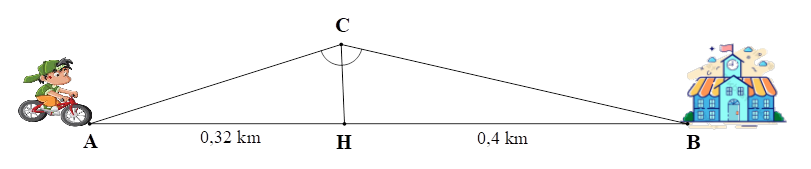
Thời gian để bạn Hải đi từ \[A\] đến \[C\] là: \[6\] giờ \[30\] phút \( - \,\,6\) giờ \[ = 30\] phút \[ = 0,5\] giờ.
Quãng đường mà bạn Hải đi từ \[A\] đến \[C\] trong \(0,5\) giờ với tốc độ trung bình lên dốc 4 km/h là: \[AC = {S_{A \to C}} = 4 \cdot 0,5 = 2\] (km).
Xét \(\Delta ACB\) có \[CH\] là đường phân giác của \(\widehat {ACB},\) nên ta có: \(\frac{{HA}}{{HB}} = \frac{{CA}}{{CB}}\) hay \(\frac{{0,32}}{{0,4}} = \frac{2}{{CB}}\) Suy ra \(CB = \frac{{0,4 \cdot 2}}{{0,32}} = 2,5\) (km).
Thời gian để bạn Hải đi hết quãng đường \(2,5\) km với tốc độ trung bình xuống dốc 10 km/h là: \(\frac{{2,5}}{{10}} = 0,25\) (giờ).
Như vậy, tổng thời gian bạn Hải đi từ \[A\] đến trường \[B\] là
\[0,5 + 0,25 = 0,75\] (giờ) \[ = 45\] (phút).
Lời giải
Hướng dẫn giải
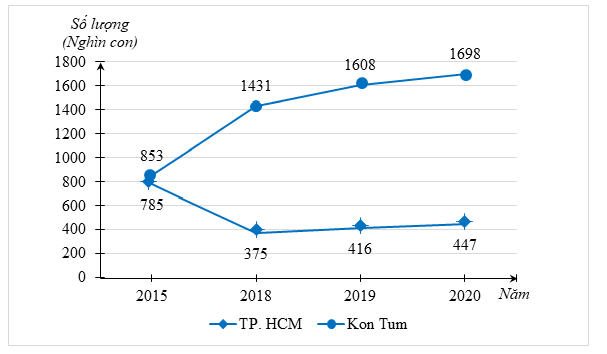
a) Ta lập được bảng thống kê như sau:
|
Năm |
2015 |
2018 |
2019 |
2020 |
|
TP. HCM |
\(785\) |
\(375\) |
\(416\) |
\(447\) |
|
Kon Tum |
\(853\) |
\(1\,\,431\) |
\(1\,\,608\) |
\(1\,\,698\) |
Ta lựa chọn biểu đồ hình cột kép để biểu diễn dữ liệu trong biểu đồ đoạn thẳng như sau:
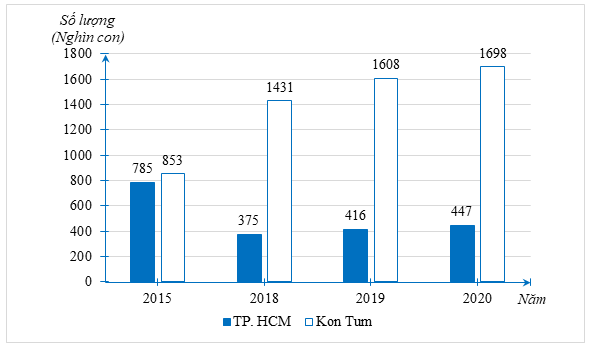
b) Trong năm 2020 lượng gia cầm ở Kon Tum nhiều nhất, là 1698 nghìn con.
c) Tổng số lượng gia cầm ở Kon Tum trong năm \[2015,\]\[2018,{\rm{ }}2019,{\rm{ }}2020\] là:
\(853 + 1\,\,431 + 1\,\,608 + 1\,\,698 = 5\,\,590\) (nghìn con).
Trong năm 2018, số lượng gia cầm ở TP. HCM \[(375\] nghìn con) ít hơn so với số lượng gia cầm ở Kon Tum \[(1{\rm{ }}431\] nghìn con) nên nhận định trên bài báo không chính xác.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
C. \(\frac{{DE}}{{AC}} = \frac{{BC}}{{BE}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.