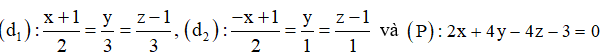Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình vuông cạnh \(a,\) cạnh bên \[SA\] vuông góc với mặt phẳng đáy, \(SA = a\sqrt 2 .\) Gọi \[M,\,\,N\] lần lượt là hình chiếu vuông góc của điểm \(A\) trên các cạnh \[SB,\,\,SD.\] Góc giữa mặt phẳng \[\left( {AMN} \right)\] và đường thẳng \[SB\] bằng:
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình vuông cạnh \(a,\) cạnh bên \[SA\] vuông góc với mặt phẳng đáy, \(SA = a\sqrt 2 .\) Gọi \[M,\,\,N\] lần lượt là hình chiếu vuông góc của điểm \(A\) trên các cạnh \[SB,\,\,SD.\] Góc giữa mặt phẳng \[\left( {AMN} \right)\] và đường thẳng \[SB\] bằng:
Quảng cáo
Trả lời:
Ta có \(BC \bot \left( {SAB} \right) \Rightarrow BC \bot AM\)
\( \Rightarrow AM \bot \left( {SBC} \right) \Rightarrow AM \bot SC.\)
Tương tự ta cũng có \(AN \bot SC \Rightarrow \left( {AMN} \right) \bot SC.\)
Gọi \(\varphi \) là góc giữa đường thẳng SB và \(\left( {AMN} \right)\)
Chuẩn hóa và chọn hệ trục tọa độ sao cho: \(D\left( {1\,;\,\,0\,;\,\,0} \right)\),
\(S\left( {0\,;\,\,0\,;\,\,\sqrt 2 } \right),\,\,C\left( {1\,;\,\,1\,;\,\,0} \right),\)\(A\left( {0\,;\,\,0\,;\,\,0} \right),\,\,\)\(B\left( {0\,;\,\,1\,;\,\,0} \right),\,\,\)\(\overrightarrow {SC} = \left( {1\,;\,\,1\,;\,\, - \sqrt 2 } \right),\,\,\overrightarrow {SB} = \left( {0\,;\,\,1\,;\,\, - \sqrt 2 } \right).\)
Do \(\left( {AMN} \right) \bot SC\) nên \(\left( {AMN} \right)\) có vectơ pháp tuyến \(\overrightarrow {SC} .\)
Do đó \(\sin \varphi = \frac{{\left| 3 \right|}}{{2\sqrt 3 }} = \frac{{\sqrt 3 }}{2} \Rightarrow \varphi = 60^\circ {\rm{. }}\)Chọn D.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Nếu gửi ở ngân hàng có lãi suất \(6\% /\)năm thì sau 2 năm số tiền cả vốn lẫn lãi thu được là: \(50{\left( {1 + \frac{6}{{100}}} \right)^2} = 56,18\) (triệu đồng).
Đáp án cần nhập là: 56,18.
Câu 2
Lời giải
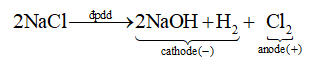
Chọn A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.