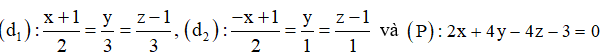Cho tứ diện \[ABCD\] có \[AB,\,\,AC,\,\,AD\] đôi một vuông góc với nhau và \(AB = AC = AD = 2a.\) Gọi \(E\) và \(F\) lần lượt là trung điểm của \[BC,\,\,BD.\] Thể tích của khối chóp \[A.EFDC\] bằng
Cho tứ diện \[ABCD\] có \[AB,\,\,AC,\,\,AD\] đôi một vuông góc với nhau và \(AB = AC = AD = 2a.\) Gọi \(E\) và \(F\) lần lượt là trung điểm của \[BC,\,\,BD.\] Thể tích của khối chóp \[A.EFDC\] bằng
Quảng cáo
Trả lời:
Thể tích khối tứ diện \[ABCD\] là:
\({V_{ABCD}} = \frac{1}{3}AD \cdot {S_{ABC}} = \frac{1}{6}AD.AB \cdot AC = \frac{4}{3}{a^3}.\)
Ta có \(\frac{{{V_{BAFE}}}}{{{V_{ABCD}}}} = \frac{{BF}}{{BD}} \cdot \frac{{BE}}{{BC}} = \frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4} \Rightarrow {V_{BAFE}} = \frac{1}{4}{V_{ABCD}}.\)
Thể tích khối chóp \[A.EFDC\] là:
\({V_{A \cdot EFDC}} = {V_{ABCD}} - {V_{BAFE}} = {V_{ABCD}} - \frac{1}{4}{V_{ABCD}} = \frac{3}{4}{V_{ABCD}} = {a^3}.\) Chọn A.
![Cho tứ diện ABCD có AB,AC,AD\] đôi một vuông góc với nhau (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/blobid14-1768898669.png)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Nếu gửi ở ngân hàng có lãi suất \(6\% /\)năm thì sau 2 năm số tiền cả vốn lẫn lãi thu được là: \(50{\left( {1 + \frac{6}{{100}}} \right)^2} = 56,18\) (triệu đồng).
Đáp án cần nhập là: 56,18.
Câu 2
Lời giải
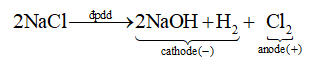
Chọn A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.