Đọc đoạn trích sau đây và trả lời câu hỏi:
Thôn Đoài ngồi nhớ thôn Đông
Một người chín nhớ mười mong một người.
Gió mưa là bệnh của giời
Tương tư là bệnh của tôi yêu nàng.
Hai thôn chung lại một làng,
Cớ sao bên ấy chẳng sang bên này?.
(Tương tư – Nguyễn Bính)
Biện pháp tu từ nào được sử dụng trong câu thơ “Thôn Đoài ngồi nhớ thôn Đông”?
Đọc đoạn trích sau đây và trả lời câu hỏi:
Thôn Đoài ngồi nhớ thôn Đông
Một người chín nhớ mười mong một người.
Gió mưa là bệnh của giời
Tương tư là bệnh của tôi yêu nàng.
Hai thôn chung lại một làng,
Cớ sao bên ấy chẳng sang bên này?.
(Tương tư – Nguyễn Bính)
Biện pháp tu từ nào được sử dụng trong câu thơ “Thôn Đoài ngồi nhớ thôn Đông”?
Quảng cáo
Trả lời:
Câu thơ sử dụng biện pháp tu từ hoán dụ: dùng địa danh để chỉ người sống trên địa danh đó: Thôn Đoài - Thôn Đông → Cách biểu đạt tình cảm kín đáo, ý nhị. Chọn C.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Nếu gửi ở ngân hàng có lãi suất \(6\% /\)năm thì sau 2 năm số tiền cả vốn lẫn lãi thu được là: \(50{\left( {1 + \frac{6}{{100}}} \right)^2} = 56,18\) (triệu đồng).
Đáp án cần nhập là: 56,18.
Câu 2
Lời giải
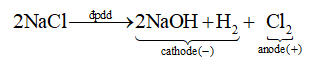
Chọn A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.